题目内容
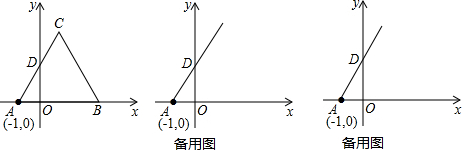
已知点A（-1，0），点B（与A不重合）在射线AO上，点C在x轴上方，且△ABC为等边三角形，射线AC交y轴于D．
（1）当AB=4时，则点B、C、D的坐标分别是：B：
（2）若AB=m（m＞0），则点B、C的坐标分别是：B：
当C、D不重合时，请根据m的不同取值，对于过B、C、D三点的二次函数开口方向作出判断，直接写出结论（不要求证明）．
（3）是否存在点B，使S△BCD=
？若存在，求出点B的坐标；若不存在，请说明理由．
（1）当AB=4时，则点B、C、D的坐标分别是：B：
（3，0）
（3，0）
，C：（1，2
）
| 3 |
（1，2
）
，D：| 3 |
（0，
）
| 3 |
（0，
）
；| 3 |
（2）若AB=m（m＞0），则点B、C的坐标分别是：B：
（m-1，0）
（m-1，0）
，C：（
m-1，
m）
| 1 |
| 2 |
| ||
| 2 |
（
m-1，
m）
；| 1 |
| 2 |
| ||
| 2 |
当C、D不重合时，请根据m的不同取值，对于过B、C、D三点的二次函数开口方向作出判断，直接写出结论（不要求证明）．
（3）是否存在点B，使S△BCD=
3
| ||
| 16 |
分析：（1）由点A（-1，0）及AB=4，易得出B点坐标为（3，0）；过点C作CE⊥x轴于点E，根据等边三角形的性质求出，AE=
AB=2，CE=
AE=2
，则OE=1，得到C点坐标为（1，2
）；解Rt△AOD，得出OD=OA•tan60°=
，进而得到D点坐标为（0，
）；
（2）先由AB=m，点A（-1，0），得出B（m-1，0）；过点C作CE⊥x轴于点E，根据等边三角形的性质得出，AE=
AB=
m，CE=
AE=
m，由两点间的距离公式求出点E（
m-1，0），则C点坐标为（
m-1，
m）；先由已知条件得出m≠1且m≠2，再分两种情况进行讨论：①0＜m＜1，②m＞1（m≠2），根据B、C、D三点的位置及抛物线的形状特征，即可得到过B、C、D三点的二次函数的开口方向；
（3）设AB=m，分两种情况进行讨论：
①当m＞2时，如备用图1，先根据三角形的面积公式得出S△BCD=S△ABC-SABD=
m2-
m，再列出方程
m2-
m=
，解方程即可求出点B1的坐标；
②当0＜m＜2时，如备用图2，先根据三角形的面积公式得出S△BCD=S△ABD-SABC=-
m2+
m，再解方程-
m2+
m=
，解方程即可．
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
（2）先由AB=m，点A（-1，0），得出B（m-1，0）；过点C作CE⊥x轴于点E，根据等边三角形的性质得出，AE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
（3）设AB=m，分两种情况进行讨论：
①当m＞2时，如备用图1，先根据三角形的面积公式得出S△BCD=S△ABC-SABD=
| ||
| 4 |
| ||
| 2 |
| ||
| 4 |
| ||
| 2 |
3
| ||
| 16 |
②当0＜m＜2时，如备用图2，先根据三角形的面积公式得出S△BCD=S△ABD-SABC=-
| ||
| 4 |
| ||
| 2 |
| ||
| 4 |
| ||
| 2 |
3
| ||
| 16 |
解答：解：（1）∵点A（-1，0），点B（与A不重合）在射线AO上，AB=4，
∴B点坐标为（3，0）；
过点C作CE⊥x轴于点E，
∵△ABC为等边三角形，
∴AE=
AB=2，CE=
AE=2
，
∴OE=AE-OA=2-1=1，
∴C点坐标为（1，2
）；
在△AOD中，∵∠AOD=90°，∠OAD=60°，OA=1，
∴OD=OA•tan60°=
，
∴D点坐标为（0，
）；
（2）∵AB=m，点A（-1，0），
∴B（m-1，0）；
过点C作CE⊥x轴于点E，
∵△ABC为等边三角形，
∴AE=
AB=
m，CE=
AE=
m，
∵点A（-1，0），
∴点E（
m-1，0），
C点坐标为（
m-1，
m）．
∵C、D不重合，
∴m≠2，
又m=1时，B与O重合，过B、C、D三点的二次函数不存在，
∴m≠1且m≠2．
当0＜m＜1时，B点在x轴负半轴上，过B、C、D三点的抛物线开口向上；
当m＞1（m≠2）时，B点在x轴正半轴上，过B、C、D三点的抛物线开口向下；
（3）存在点B，使S△BCD=
．理由如下：
设AB=m，分两种情况：
①当m＞2时，如备用图1．
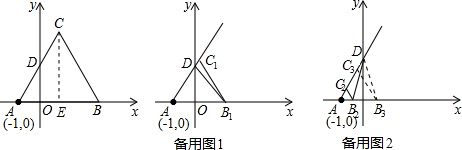S△BCD=S△ABC-SABD=
m2-
m•
=
m2-
m，
由
m2-
m=
，
解得m1=
，m2=
（不满足m＞2，舍去），
所以有m=
，-1+
=
，
这时点B1的坐标为（
，0）；
②当0＜m＜2时，如备用图2，S△BCD=S△ABD-SABC=
m•
-
m2=-
m2+
m，
由-
m2+
m=
，
解得m1=
，m2=
，
-1+
=-
，-1+
=
，
这时点B2的坐标为（-
，0），点B3的坐标为（
，0）．
综上所述，当点B的坐标为（
，0），（-
，0）和（
，0）时，有S△BCD=
．
故答案为（3，0），（1，2
），（0，
）；（m-1，0），（
m-1，
m）．
∴B点坐标为（3，0）；
过点C作CE⊥x轴于点E，
∵△ABC为等边三角形，
∴AE=
| 1 |
| 2 |
| 3 |
| 3 |
∴OE=AE-OA=2-1=1，
∴C点坐标为（1，2
| 3 |
在△AOD中，∵∠AOD=90°，∠OAD=60°，OA=1，
∴OD=OA•tan60°=
| 3 |
∴D点坐标为（0，
| 3 |
（2）∵AB=m，点A（-1，0），
∴B（m-1，0）；
过点C作CE⊥x轴于点E，
∵△ABC为等边三角形，
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
∵点A（-1，0），
∴点E（
| 1 |
| 2 |
C点坐标为（
| 1 |
| 2 |
| ||
| 2 |
∵C、D不重合，
∴m≠2，
又m=1时，B与O重合，过B、C、D三点的二次函数不存在，
∴m≠1且m≠2．
当0＜m＜1时，B点在x轴负半轴上，过B、C、D三点的抛物线开口向上；
当m＞1（m≠2）时，B点在x轴正半轴上，过B、C、D三点的抛物线开口向下；
（3）存在点B，使S△BCD=
3
| ||
| 16 |
设AB=m，分两种情况：
①当m＞2时，如备用图1．
S△BCD=S△ABC-SABD=
| ||
| 4 |
| 1 |
| 2 |
| 3 |
| ||
| 4 |
| ||
| 2 |
由
| ||
| 4 |
| ||
| 2 |
3
| ||
| 16 |
解得m1=
2+
| ||
| 2 |
2-
| ||
| 2 |
所以有m=
2+
| ||
| 2 |
2+
| ||
| 2 |
| ||
| 2 |
这时点B1的坐标为（
| ||
| 2 |
②当0＜m＜2时，如备用图2，S△BCD=S△ABD-SABC=
| 1 |
| 2 |
| 3 |
| ||
| 4 |
| ||
| 4 |
| ||
| 2 |
由-
| ||
| 4 |
| ||
| 2 |
3
| ||
| 16 |
解得m1=
| 1 |
| 2 |
| 3 |
| 2 |
-1+
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
这时点B2的坐标为（-
| 1 |
| 2 |
| 1 |
| 2 |
综上所述，当点B的坐标为（
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
3
| ||
| 16 |
故答案为（3，0），（1，2
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
点评：本题考查了等边三角形的性质，解直角三角形，二次函数的性质，两点间的距离公式，三角形的面积，解一元二次方程等知识，综合性较强，难度适中，运用数形结合及分类讨论思想是解题的关键．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
14、如图，已知点A，B，C在⊙O上，AC∥OB，∠BOC=40°，则∠ABO=
2，A3的横坐标依次为三个连续整数，其他条件不变，求线段CA2的长．