题目内容
【题目】如图,AD是△ABC的角平分线,点E是AB边上一点,AE=AC,EF∥BC,交AC于点F.下列结论正确的是( )
①∠ADE=∠ADC;②△CDE是等腰三角形;③CE平分∠DEF;④AD垂直平分CE;⑤AD=CE.

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
根据三角形全等和等腰三角形的判定、垂直平分线的判定进行依次判定即可.
解:①∵AD是△ABC的角平分线,
∴∠EAD=∠CAD,
在△AED和△ACD中,
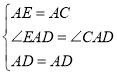 ,
,
∴△AED≌△ACD,
∴∠ADE=∠ADC
故①正确;
②∵△AED≌△ACD,
∴ED=DC,
∴△CDE是等腰三角形;
故②正确;
③∵DE=DC,
∴∠DEC=∠DCE,
∵EF∥BC,
∴∠DCE=∠CEF,
∴∠DEC=∠CEF,
∴CE平分∠DEF,
故③正确;
④∵DE=DC,
∴点D在线段EC的垂直平分线上,
∵AE=AC,
∴点A在线段EC的垂直平分线上,
∴AD垂直平分CE.
故④正确;
⑤∵AD垂直平分CE,
∴当四边形ACDE是矩形时,AD=CE,
故⑤不正确;
故选:B.

练习册系列答案
相关题目