��Ŀ����
����Ŀ����ͼ������ֽ��ÿ��С�����εı߳����ǵ�λ1����ABC���������㶼�ڸ���ϣ����������ƽ��ֱ������ϵ����������⣺
��1������ABC����ƽ��3����λ����������ƽ��2����λ���ȣ���������ƽ�ƺ�ġ�A1B1C1��
��2��д��A1��C1�����ꣻ
��3������A1B1C1��C1��ʱ����ת90�㣬������ת��ġ�A2B2C1�����߶�B1C1��ת������ɨ�����������������У���
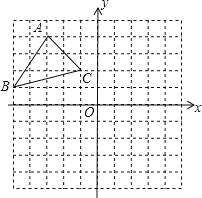
���𰸡���1����ͼ����������2��A1��0��2����C1��2��0������3��![]() ��
��
��������
�����������1������ͼ��ƽ�Ƶ����ʻ�������ƽ�ƺ�ġ�A1B1C1���ɣ�
��2�����ݡ�A1B1C1������ϵ�е�λ��д��A1��C1�����ꣻ
��3������ͼ����ת�����ʻ�����ת��ġ�A2B2C1���ٸ��ݹ��ɶ������B1C1�ij��������ε������ʽ���ɼ�����߶�B1C1��ת������ɨ���������
�����������1����ͼ��ʾ��
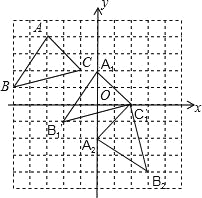
��2���ɡ�A1B1C1������ϵ�е�λ�ÿ�֪��A1��0��2����C1��2��0����
��3����ת���ͼ����ͼ��ʾ��
���ɹ��ɶ�����֪��B1C1=![]() ��
��
��S����=![]() ��
��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ