Question

【题目】为创办“生活宜居城市”，平原县委县府把主要路段路灯更换为节能路灯．已知节能路灯售价为5000元/个，目前两个商家有此产品．甲商家用如下方法促销：若购买路灯不超过100个，按原价付款；若一次购买1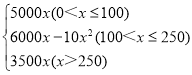00个以上，且购买的个数每增加一个，其价格减少10元，但节能路灯的售价不得低于3500元/个．乙店一律按原价的80℅销售．现购买节能路灯x个，如果全部在甲商家购买，则所需金额为y1元；如果全部在乙商家购买，则所需金额为y2元.

（1）分别求出y1、y2与x之间的函数关系式；

（2）若县委县府投资140万元，最多能购买多少个节能路灯？

Answer 1

【答案】（1）y1=，y2=5000×80%x=4000x．（2）最多能购买400个路灯．

【解析】

试题分析：（1）对甲，由于购买个数不同，售价也不同，因此需按购买个数分成三段由等量关系“所需金额=售价×购买个数”列出函数关系式；

对乙，按等量关系“所需金额=售价×购买个数”列出函数关系式．

（2）分别计算投资额在甲乙商家各能购买的太阳能路灯的数量，比较得出最大值．

试题解析：（1）由题意可知，

当0＜x≤100时，购买一个需5000元，故y1=5000x；

当x＞100时，

∵购买个数每增加一个，其价格减少10元，但售价不得低于3500元/个，

∴x≤+100=250个．

即100＜x≤250时，购买一个需5000-10（x-100）元，

故y1=-10x2+6000x；

当x＞250时，购买一个需3500元，

故y1=3500x；

∴y1=，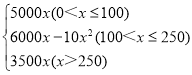

y2=5000×80%x=4000x．

（2）在甲商家，当0＜x≤100时，y1=5000x≤500000＜1400000；

当100＜x≤250时，y1=6000x-10x2=-10（x-300）2+900000＜1400000；

∴由3500x=1400000，得x=400；

在乙商家，由4000x=1400000，

得x=350个．

故选择甲商家，最多能购买400个路灯．