Question

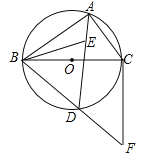
【题目】已知：如图，⊙O与⊙P相交于A、B两点，点P在⊙O上，⊙O的弦AC切⊙P于点A，CP及其延长线交⊙P于D、E，过点E作EF⊥CE交CB的延长线于F．

（1）求证：BC是⊙P的切线；

（2）若CD＝2，CB＝2，求EF的长．

Answer 1

【答案】（1）见解析（2）

【解析】

（1）连接PA，PB，根据圆内接四边形对角互补证明∠PBC是直角，从而可以确定CB是⊙P的切线；
（2）根据△FCE∽△PCB，则，由于CB是⊙P的切线，所以根据CB2=CD（CD+DE），可以求得DE的长度，进而求得CE的长度；再求得BP的长度即可，在Rt△CPB中，CP=3，CB=2，则可求得EF的长度．

（1）连接PB，PA，

∵点P在⊙O上，

∵⊙O的弦AC切⊙P于点A，

∴∠CAP＝90°，

∵四边形APBC是⊙O的内接四边形，

∴∠PBC＝90°，即PB⊥CB．

∵B在⊙P上，

∴CB是⊙P的切线．

（2）∵CB是⊙P的切线，

∴CB2＝CD（CD+DE）．

∵CD＝2，CB＝，

∴（2）2═2×（2+ED）．

∴DE＝2．

∴CE＝CD+DE＝2+2＝4．

∴在⊙P中，PD＝PE＝ED＝1，

∵CP＝3，CB＝2，

∴BP＝1．

∵EF⊥CE，

∴∠FEC＝∠CBP＝90°，∠FCE＝∠PCB．

∴△FCE∽△PCB．

∴，

∵CB＝2，CE＝4，BP＝1，

∴，

∴EF＝．