题目内容
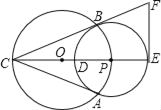
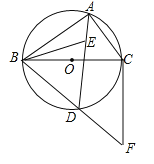
【题目】如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.
(1)求证:DB=DE;
(2)求证:直线CF为⊙O的切线.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)欲证明DB=DE,只要证明∠DBE=∠DEB;
(2)欲证明直线CF为⊙O的切线,只要证明BC⊥CF即可;
试题解析:(1)证明:∵E是△ABC的内心,∴∠BAE=∠CAE,∠EBA=∠EBC,∵∠BED=∠BAE+∠EBA,∠DBE=∠EBC+∠DBC,∠DBC=∠EAC,∴∠DBE=∠DEB,∴DB=DE.
(2)连接CD.∵DA平分∠BAC,∴∠DAB=∠DAC,∴![]() ,∴BD=CD,∵BD=DF,∴CD=DB=DF,∴∠BCF=90°,∴BC⊥CF,∴CF是⊙O的切线.
,∴BD=CD,∵BD=DF,∴CD=DB=DF,∴∠BCF=90°,∴BC⊥CF,∴CF是⊙O的切线.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目