��Ŀ����
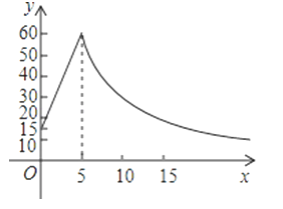
����Ŀ����ͼ��ʾ������һ�ֲ�Ʒ��ͬʱ����Ҫ��ԭ���ϼ��ȣ���ò����¶�Ϊy�棬�Ӽ��ȿ�ʼ�����ʱ��Ϊx���ӣ����˽⣬�ò����ڼ��ȹ������¶�y��ʱ��x��һ�κ�����ϵ����֪�ò����ڼ���ǰ���¶�Ϊ15�棬����5����ʹ�����¶ȴﵽ60��ʱֹͣ���ȣ�ֹͣ���Ⱥ����¶����½�����ʱ�¶�y��ʱ��x�ɷ�����������ϵ��
��1���ֱ�����ò��ϼ��ȹ����к�ֹͣ���Ⱥ�y��x֮��ĺ�������ʽ����д��x��ȡֵ��Χ��
��2�����ݹ���Ҫ���ڲ����¶Ȳ�����30������ʱ���ڣ���Ҫ�Ըò��Ͻ������������ô�Ըò��Ͻ�����������õ�ʱ���Ƕ��٣�
���𰸡���1��y=9x+15��0��x��5����y=![]() ��x��5������2��
��x��5������2��![]() ���ӣ�
���ӣ�
��������
��1��ȷ�������������ҵ�����ͼ���ĵ�����꣬�ô���ϵ������ú����Ľ���ʽ���ɣ�
��2���ֱ������������ĺ���ֵΪ30���������x��ֵ������ɵõ��𰸣�
��1������ȹ�����һ�κ�������ʽΪy=kx+b��k��0�����ú���ͼ���㣨0��15������5��60������![]() ����ã�
����ã�![]() ����һ�κ����ı���ʽΪy=9x+15��0��x��5���������ֹͣ������������ʽΪy
����һ�κ����ı���ʽΪy=9x+15��0��x��5���������ֹͣ������������ʽΪy![]() ��a��0�����ú���ͼ���㣨5��60������
��a��0�����ú���ͼ���㣨5��60������![]() 60����ã�a=300�����Է�������������ʽΪy
60����ã�a=300�����Է�������������ʽΪy![]() ��x��5����
��x��5����
��2��������ã�![]() ����ã�x1
����ã�x1 ����ã�x2=10����x2��x1=10
����ã�x2=10����x2��x1=10![]() �����ԶԸò��Ͻ�����������õ�ʱ��Ϊ
�����ԶԸò��Ͻ�����������õ�ʱ��Ϊ![]() ���ӣ�
���ӣ�

 ��У����ϵ�д�
��У����ϵ�д�






