题目内容
【题目】(本题满分10分)如图,在平面直角坐标系中,抛物线y=ax2+bx+4与x轴的一个交点为A(-2,0),与y轴的交点为C,对称轴是x=3,对称轴与x轴交于点B.
(1)求抛物线的函数表达式;
(2)经过B,C的直线l平移后与抛物线交于点M,与x轴交于点N,当以B,C,M,N为顶点的四边形是平行四边形时,求出点M的坐标.
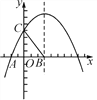
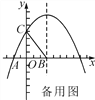
【答案】(1) 抛物线的表达式为y=-x2+x+4 ;(2) M的坐标为(6,4)或(3-![]() ,-4)或(3+
,-4)或(3+![]() ,-4).
,-4).
【解析】解:(1)∵抛物线y=ax2+bx+4交x轴于A(-2,0),∴0=4a-2b+4,∵对称轴是直线x=3,∴-![]() =3,即6a+b=0,关于a,b的方程联立解得 a=-,b=,∴抛物线的表达式为y=-x2+x+4 (2)∵四边形为平行四边形,且BC∥MN,∴BC=MN.①N点在M点下方,即M点向下平移4个单位,向右平移3个单位与N重合.设M1(x,- x2+x+4),则N1(x+3,- x2+x),∵N1在x轴上,∴-x2+x=0,解得 x=0(M与C重合,舍去),或x=6,∴xM=6,∴M1(6,4);②M点在N点右下方,即N向下平移4个单位,向右平移3个单位与M重合.设M(x,- x2+x+4),则N(x-3,- x2+x+8),∵N在x轴上,∴-x2+x+8=0,解得 x=3-
=3,即6a+b=0,关于a,b的方程联立解得 a=-,b=,∴抛物线的表达式为y=-x2+x+4 (2)∵四边形为平行四边形,且BC∥MN,∴BC=MN.①N点在M点下方,即M点向下平移4个单位,向右平移3个单位与N重合.设M1(x,- x2+x+4),则N1(x+3,- x2+x),∵N1在x轴上,∴-x2+x=0,解得 x=0(M与C重合,舍去),或x=6,∴xM=6,∴M1(6,4);②M点在N点右下方,即N向下平移4个单位,向右平移3个单位与M重合.设M(x,- x2+x+4),则N(x-3,- x2+x+8),∵N在x轴上,∴-x2+x+8=0,解得 x=3-![]() ,或x=3+
,或x=3+![]() ,∴xM=3-
,∴xM=3-![]() 或3+
或3+![]() .∴M2(3-
.∴M2(3-![]() ,-4)或M3(3+
,-4)或M3(3+![]() ,-4).综上所述,M的坐标为(6,4)或(3-
,-4).综上所述,M的坐标为(6,4)或(3-![]() ,-4)或(3+
,-4)或(3+![]() ,-4)
,-4)

练习册系列答案
相关题目