题目内容
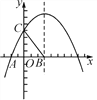
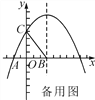
【题目】如图,已知抛物线![]() 和直线
和直线![]() 都经过A(1,0),B(﹣2,3)两点.
都经过A(1,0),B(﹣2,3)两点.
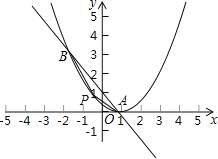
(1)求抛物线y1及直线y2的解析式;
(2)点P是抛物线上一动点,在直线AB的下方,当△PAB的面积最大时,请求出P点坐标;
(3)抛物线上是否存在一点M,使△MAB与△OAB的面积相等?若存在,请求出M点的坐标;若不存在,请说明理由.
【答案】(1)![]() ,
, ![]() ;(2)
;(2)![]() ;(3)
;(3)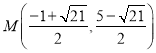 或
或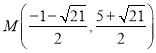
【解析】 (1)由抛物线和直线均过点A、B,由待定系数法即可求出二者的解析式;
(2)寻找与直线AB平行的直线l,使l与抛物线相切于点P时,的面积,由可求出直线l的解析式,代入即可求出P点的值;
(3)假设存在,由的面积与相等可以知道点M与点O到直线AB的距离相等,结合点到直线的距离即可求出点M的坐标.
本题解析:
(1)![]() ,
,
![]() ;
;
(2)设![]() ,得
,得![]() ,所以当
,所以当![]() 时,面积最大;此时
时,面积最大;此时![]() ;
;
(3)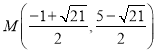 或
或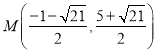

练习册系列答案
相关题目