��Ŀ����
����Ŀ������ABC�У���ACB=90����AC=BC��ֱ��MN������C����AD��MN��D��BE��MN��E.
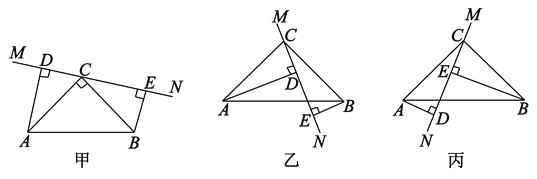
(1)��ֱ��MN�Ƶ�C��ת��ͼ��λ��ʱ����˵��������ADC�ա�CEB����DE=AD��BE��
(2)��ֱ��MN�Ƶ�C��ת��ͼ�ҵ�λ��ʱ����˵����DE=AD��BE��
(3)��ֱ��MN�Ƶ�C��ת��ͼ����λ��ʱ������DE��AD��BE���������ĵ�����ϵ����д�����������ϵ��������֤����
���𰸡���1��֤��������������֤������������3��AD��DE��BE������ĵ�����ϵ��DE=BE��AD(��AD=BE��DE��BE=AD��DE��)���ɼ�����.
�������������������1���ɡ�ACB=90�����á�BCE����ACD=90������AD��MN��D��BE��MN��E.���ADC=��CEB=90�������ݵȽǵ������ȵõ���ACD=��CBE.����
Rt��ADC��Rt��CEB������AD=CE��DC=BE�����ɵõ�DE=DC+CE=BE+AD��
��2�����ݵȽǵ������ȵõ���ACD=��CBE���á�ADC�ա�CEB,�õ�AD=CE��DC=BE������DE=CE-CD=AD-BE��
��3��DE��AD��BE���еĵ�����ϵΪ��DE=BE-AD��֤���ķ����루2����ͬ��
���������(1)�١ߡ�ACB=90����
���ACD+��BCE=90����
��AD��MN��D��BE��MN��E��
���ADC=��CEB=90������BCE+��CBE=90����
���ACD=��CBE.
�ڡ�ADC�͡�CEB��, 
���ADC�ա�CEB(AAS)��
�ڡߡ�ADC�ա�CEB��
��CE=AD��CD=BE��
��DE=CE��CD=AD��BE��
(2)�ߡ�ADC=��CEB=��ACB=90����
���ACD=��CBE.�֡�AC=BC��
���ADC�ա�CEB(AAS)��
��CD=BE.AD=CE��
��DE=CE��CD=AD��BE��
(3)��MN��ת��ͼ����λ��ʱ��AD��DE��BE������ĵ�����ϵ��DE=BE��AD(��AD=BE��DE��BE=AD��DE��)��
�ߡ�ADC=��CEB=��ACB=90����
���ACD=��CBE.
��AC=BC��
���ACD�ա�CBE(AAS)��
��AD=CE��CD=BE��
��DE=CD��CE=BE��AD.




