题目内容
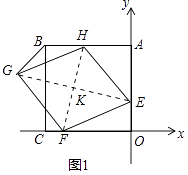
【题目】如图1,在平面直角坐标系中,正方形ABCO的顶点C、A分别在x、y轴上,A(0,6)、E(0,2),点H、F分别在边AB、OC上,以H、E、F为顶点作菱形EFGH
(1)当H(﹣2,6)时,求证:四边形EFGH为正方形
(2)若F(﹣5,0),求点G的坐标
(3)如图2,点Q为对角线BO上一动点,D为边OA上一点,DQ⊥CQ,点Q从点B出发,沿BO方向移动.若移动的路径长为3,直接写出CD的中点M移动的路径长为 .
【答案】
(1)
证明:如图1中,
∵E(0,2),H(﹣2,6),
∴OE=AH=2,
∵四边形ABCO是正方形,
∴∠HAE=∠EOF=90°,
∵四边形EFGH是菱形,
∴EH=EF,
在Rt△AHE和Rt△OEF中,
![]() ,
,
∴Rt△AHE≌△Rt△OEF,
∴∠AEH=∠EFO,
∵∠EFO+∠FEO=90°,
∴∠AEH+∠FEO=90°,
∴∠HEF=90°,
∴四边形EFGH是正方形
(2)
解:如图1中,连接GE、FH交于点K.
∵F(﹣5,0),E(0,2),
∴OF=5,OE=2,EA=4,
∵HE=EF,
∴52+22=42+AH2,
∴AH= ![]() ,
,
∴H(﹣ ![]() ,6),
,6),
∵四边形EFGH是菱形,
∴HK=KF,KE=KG,设G(m,n),则有 ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴m=﹣5﹣ ![]() ,n=4,
,n=4,
∴G(﹣5﹣ ![]() ,4)
,4)
(3)![]()
【解析】(3)解:如图2中,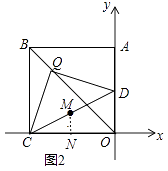
如图2中,作MN⊥CO于M.
∵MN∥OD,CM=MD,
∴CN=ON,
∴MN垂直平分线段CO,
∴点M在线段OC的垂直平分线上运动,
如图3中,易知当点Q与B重合时,点M与BD的中点N重合,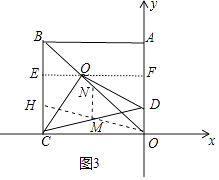
当BQ=3时,作EQ⊥BC于E,延长EQ交OA于F,延长OM交BC于H,连接NM(线段MN的长即为点M的运动轨迹的长),
∵QC=QD,∠CEQ=∠QFD,易证∠ECQ=∠FQD,
∴△EQC≌△FDQ,
∴EQ=DF=BE= ![]() ,CE=OF=6﹣
,CE=OF=6﹣ ![]() ,
,
∴DO=6﹣3 ![]() ,
,
∵CM=DM,∠CMH=∠OMD,∠CHM=∠DOM,
∴△HMC≌△OMD,
∴OM=HM,CH=OD=6﹣3 ![]() ,BH=3
,BH=3 ![]() ,
,
∵ON=NB,
∴MN= ![]() BH=
BH= ![]() ,
,
∴点M的运动的路径的长为 ![]() .
.
所以答案是 ![]() .
.
【考点精析】本题主要考查了菱形的性质和正方形的性质的相关知识点,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.