题目内容
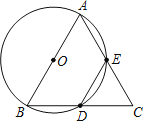
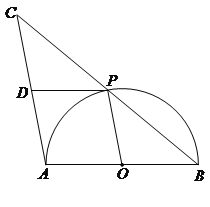
【题目】(9分)如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD,PO.
(1)求证:△CDP≌△POB;
(2)填空:
① 若AB=4,则四边形AOPD的最大面积为 ;
② 连接OD,当∠PBA的度数为 时,四边形BPDO是菱形.
【答案】(1)参见解析;(2)①4;②60º.
【解析】试题(1)利用边角边证明这两个三角形全等;(2)①当∠CAB=90时,四边形AOPD有最大面积,此时等于AO乘以AD的值;②当四边形BPDO是菱形时,可推出OB=OP=OD=DP,三角形DPO是等边三角形,所以∠PDO=60,∵菱形对角相等,∴∠PBA的度数也等于60.
试题解析:(1)∵D是AC的中点,且PC=PB,∴DP∥AB,DP=![]() AB,∴∠CPD=∠PBO,∵OB=
AB,∴∠CPD=∠PBO,∵OB=![]() AB,∴DP=OB,∴△CDP≌△POB;(2)①∵四边形AOPD是平行四边形,当高等于AD时,四边形AOPD有最大面积,此时∠CAB=90,最大面积=AO×AD=2×2=4;②当四边形BPDO是菱形时,OD=DP=OB,∵OB=OP,∴OP=OD=DP,∴△DPO是等边三角形,∴∠PDO=60,∵菱形对角相等,∴∠PBA=∠PDO=60.
AB,∴DP=OB,∴△CDP≌△POB;(2)①∵四边形AOPD是平行四边形,当高等于AD时,四边形AOPD有最大面积,此时∠CAB=90,最大面积=AO×AD=2×2=4;②当四边形BPDO是菱形时,OD=DP=OB,∵OB=OP,∴OP=OD=DP,∴△DPO是等边三角形,∴∠PDO=60,∵菱形对角相等,∴∠PBA=∠PDO=60.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目