题目内容
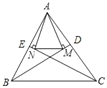
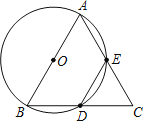
【题目】如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC、AC于点D、E,且点D为BC的中点.
(1)求证:△ABC为等边三角形;
(2)求DE的长;
(3)在线段AB的延长线上是否存在一点P,使△PBD≌△AED?若存在,请求出PB的长;若不存在,请说明理由.
【答案】(1)证明见解析;(2)1;(3)PB=1.
【解析】试题分析: ![]() 连接
连接![]() 利用直径所对的圆周角为直角及垂直平分线的性质得到相等的线段
利用直径所对的圆周角为直角及垂直平分线的性质得到相等的线段![]() 联立已知的
联立已知的![]() ,即可证得
,即可证得![]() 是等边三角形;
是等边三角形;![]() 连接
连接![]() 利用直径所对的圆周角为直角,得到
利用直径所对的圆周角为直角,得到![]() 然后利用等腰三角形三线合一的性质得出
然后利用等腰三角形三线合一的性质得出![]() 为
为![]() 的中点.利用三角形中位线的数量关系求得
的中点.利用三角形中位线的数量关系求得![]() 的长度;
的长度;![]() 根据等边三角形的性质,可以证得
根据等边三角形的性质,可以证得![]() 和
和![]() 有一组边
有一组边![]() 和一对角
和一对角![]() 对应相等,所以只要再满足这组角的另一夹边对应相等就可以了.
对应相等,所以只要再满足这组角的另一夹边对应相等就可以了.
试题解析: ![]() 证明:连接
证明:连接![]()

![]() 是
是![]() 的直径,
的直径,
![]()
∵点![]() 是
是![]() 的中点,
的中点,
![]() 是线段
是线段![]() 的垂直平分线.
的垂直平分线.
![]()
![]()
![]()
![]() 为等边三角形.
为等边三角形.
![]() 连接
连接![]()
![]() 是直径,
是直径,
![]()
![]()
![]() 是等边三角形,
是等边三角形,
![]()
即![]() 为
为![]() 的中点.
的中点.
![]() 是
是![]() 的中点,故
的中点,故![]() 为
为![]() 的中位线,
的中位线,
![]()
![]() 存在点
存在点![]() 使
使![]()
由![]() 知,
知, ![]()
![]()
![]()
![]()
![]()
![]()
要使![]()
只需![]()

练习册系列答案
相关题目
【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
|
|
|
|
|
| ··· |
![]() 可求得
可求得![]() ,第
,第![]() 个格子中的数为 ;
个格子中的数为 ;
![]() 判断:前
判断:前![]() 个格子中所填整数之和是否可能为
个格子中所填整数之和是否可能为![]() 若能,求出
若能,求出![]() 的值,若不可能,请说明理由;
的值,若不可能,请说明理由;
![]() 如果
如果![]() ,
,![]() 为前
为前![]() 格子中的任意两个数,那么所有
格子中的任意两个数,那么所有![]() 的和可以通过计算
的和可以通过计算
![]() 得到,若
得到,若![]() span>,
span>,![]() 为前
为前![]() 格子中的任意两个数,则所有
格子中的任意两个数,则所有![]() 的的和为
的的和为