题目内容
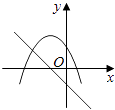
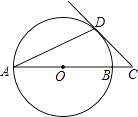
【题目】如图1,AD,BC是⊙O的两条互相垂直的直径,点P从点O出发沿图中某一个扇形顺时针匀速运动,设∠APB=y(单位:度),如果y与点P运动的时间x(单位:秒)的函数关系的图象大致如图2所示,那么点P的运动路线可能为( )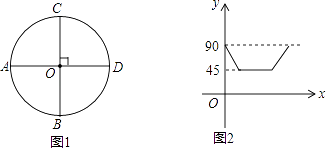
A.O→B→A→O
B.O→A→C→O
C.O→C→D→O
D.O→B→D→O
【答案】C
【解析】解:当点P沿O→C运动时,
当点P在点O的位置时,y=90°,
当点P在点C的位置时,
∵OA=OC,
∴y=45°,
∴y由90°逐渐减小到45°;
当点P沿C→D运动时,
根据圆周角定理,可得
y≡90°÷2=45°;
当点P沿D→O运动时,
当点P在点D的位置时,y=45°,
当点P在点0的位置时,y=90°,
y由45°逐渐增加到90°.
故点P的运动路线可能为O→C→D→O.
故选:C.
根据图2,分三段考虑:当点P沿O→C运动时;当点P沿C→D运动时;当点P沿D→O运动时;分别判断出y的取值情况,进而判断出y与点P运动的时间x(单位:秒)的关系即可.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案【题目】某中学八年级的篮球队有![]() 名队员.在罚篮投球训练中,这
名队员.在罚篮投球训练中,这![]() 名队员各投篮
名队员各投篮![]() 次的进球情况如下表:
次的进球情况如下表:
进球数 |
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
针对这次训练,请解答下列问题:
![]() 这
这![]() 名队员进球数的平均数是________,中位数是________;
名队员进球数的平均数是________,中位数是________;
![]() 求这支球队罚篮命中率.罚篮命中率
求这支球队罚篮命中率.罚篮命中率![]() (进球数
(进球数![]() 投篮次数)
投篮次数)![]() ________;
________;
![]() 若队员小亮的罚篮命中率为
若队员小亮的罚篮命中率为![]() ,请你分析小亮在这支球队中的罚篮水平.
,请你分析小亮在这支球队中的罚篮水平.
【题目】阅读下面材料:在数学课上,老师提出如下问题:
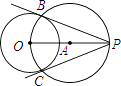
尺规作图,过圆外一点作圆的切线. |
小涵的主要作法如下:
如图,(1)连结OP,作线段OP的中点A; |
老师说:“小涵的做法是正确的.”
请回答:小涵的作图依据是 .