Question

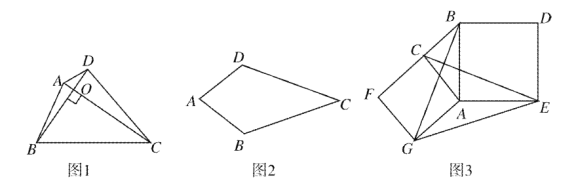
【题目】如图1，对角线互相垂直的四边形叫做垂美四边形.

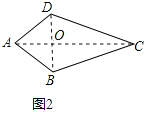
(1)概念理解：如图2，在四边形中，，问四边形是垂美四边形吗?请说明理由；

(2)性质探究：如图1，四边形的对角线交于点，.

试证明：；

(3)解决问题：如图3，分别以的直角边和斜边为边向外作正方形和正方形，连结.已知，求的长.

Answer 1

【答案】(1)是，理由见解析； (2)见解析；（3）

【解析】

（1）根据垂直平分线的判定定理证明即可；
（2）根据垂直的定义和勾股定理解答即可；
（3）根据垂美四边形的性质、勾股定理、结合（2）的结论计算．

解：（1）是

理由：，

∴在的垂直平分线上.

∵，

∴在的垂直平分线上.

∴垂直平分.

∴四边形为垂美四边形.

（2）如图2，连接AC和BD，

，

，

，

，

.

.

.

；

（3）连接CG、BE，
∵∠CAG=∠BAE=90°，
∴∠CAG+∠BAC=∠BAE+∠BAC，即∠GAB=∠CAE，
在△GAB和△CAE中，

，

∴△GAB≌△CAE（SAS），
∴∠ABG=∠AEC，又∠AEC+∠AME=90°，
∴∠ABG+∠AME=90°，即CE⊥BG，
∴四边形CGEB是垂美四边形，
由（2）得，CG2+BE2=CB2+GE2，
∵，

∴AC=，AB=2，CG=，BE=，

∴GE2=CG2+BE2-CB2=13，
∴GE=.