题目内容
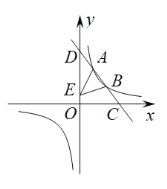
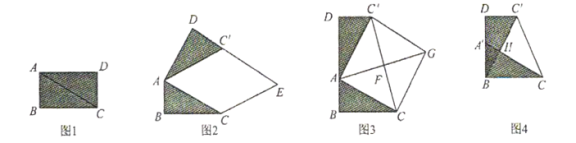
【题目】曲线![]() 在直角坐标系中的位置如图所示,曲线
在直角坐标系中的位置如图所示,曲线![]() 是由半径为2,圆心角为
是由半径为2,圆心角为![]() 的
的![]() (
(![]() 是坐标原点,点
是坐标原点,点![]() 在
在![]() 轴上)绕点
轴上)绕点![]() 旋转
旋转![]() ,得到
,得到![]() ;再将
;再将![]() 绕点
绕点![]() 旋转
旋转![]() ,得到
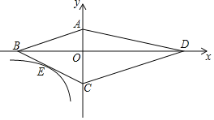
,得到![]() ;……依次类推,形成曲线
;……依次类推,形成曲线![]() ,现有一点
,现有一点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位长度的速度,沿曲线
个单位长度的速度,沿曲线![]() 向右运动,则点
向右运动,则点![]() 的坐标为___________;在第
的坐标为___________;在第![]() 时,点
时,点![]() 的坐标为____________.
的坐标为____________.
【答案】(![]() ,0) (
,0) (![]() ,0)
,0)
【解析】
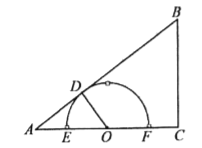
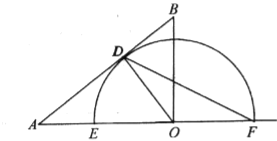
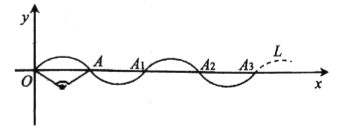
如图,设![]() 的圆心为J,过点J作JK⊥OA于K.解直角三角形求出OA的长,即可得到点A坐标,再求出点P的运动路径,判断出点P的位置,求出OP可得结论.
的圆心为J,过点J作JK⊥OA于K.解直角三角形求出OA的长,即可得到点A坐标,再求出点P的运动路径,判断出点P的位置,求出OP可得结论.
如图,设![]() 的圆心为J,过点J作JK⊥OA于K.
的圆心为J,过点J作JK⊥OA于K.
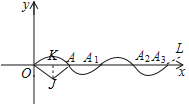
由题意JO=JA=2,∠AJO=120°,
∵JK⊥OA,
∴OK=KA,∠OJK=∠AJK=60°,
∴KO=KA=OJsin60°=![]() ,
,
∴OA=2![]() ,
,
∴A(2![]() ,0),
,0),
∵![]() 的长=
的长=![]() ,点P的运动路径=2020π,
,点P的运动路径=2020π,
又∵2020π÷![]() π=1515,
π=1515,
∴点P在x轴上,OP的长=1515×2![]() =3030
=3030![]() ,
,
∴此时P(3030![]() ,0).
,0).
故答案为(2![]() ,0),(3030
,0),(3030![]() ,0).
,0).

【题目】随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯.由此催生了一批外卖点餐平台,已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取80名点外卖的用户进行统计,按送餐距离分类统计结果如下表:
送餐距离x(千米) | 0 | 1 | 2 | 3 | 4 |
数量 | 12 | 20 | 24 | 16 | 8 |
(1)从这80名点外卖的用户中任取一名用户,该用户的送餐距离不超过3千米的概率为 ;
(2)以这80名用户送餐距离为样本,同一组数据取该小组数据的中间值(例如第二小组(1<x ≤2)的中间值是1.5),试估计利用该平台点外卖用户的平均送餐距离;
(3)若该外卖平台给送餐员的送餐费用与送餐距离有关,不超过2千米时,每份3元;超过2千米但不超4千米时,每份5元;超过4千米时,每份9元. 以给这80名用户所需送餐费用的平均数为依据,若送餐员一天的目标收入不低于150元,试估计一天至少要送多少份外卖?