题目内容
【题目】如图,某校20周年校庆时,需要在草场上利用气球悬挂宣传条幅,EF为旗杆,气球从A处起飞,几分钟后便飞达C处,此时,在AF延长线上的点B处测得气球和旗杆EF的顶点E在同一直线上.
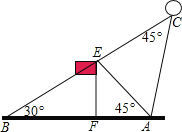
(1)已知旗杆高为12米,若在点B处测得旗杆顶点E的仰角为30°,A处测得点E的仰角为45°,试求AB的长(结果保留根号);
(2)在(1)的条件下,若∠BCA=45°,绳子在空中视为一条线段,试求绳子AC的长(结果保留根号)?
【答案】(1)12![]() +12%(米);(2)6
+12%(米);(2)6![]() +6
+6![]() (米).
(米).
【解析】
试题(1)在直角△BEF中首先求得BF,然后在直角△AEF中求得AF,根据AB=BF+AF即可求解;
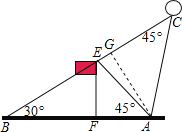
(2)作AG⊥BC于点G,在直角△ABG中首先求得AG,然后在直角△AGC中利用三角函数求解.
解:(1)∵在直角△BEF中,tan∠EBF=![]() ,
,
∴BE=![]()
![]() =
=![]() =12
=12![]() .
.
同理AF=EF=12(米),
则AB=BF+AF=12![]() +12%(米);
+12%(米);
(2)作AG⊥BE于点G,
在直角△ABG中,AG=ABsin30°=![]() (12
(12![]() +12)=6
+12)=6![]() +6.
+6.
又∵直角△AGC中,∠ACG=45°,
∴AC=![]() AG=6
AG=6![]() +6
+6![]() (米).
(米).

练习册系列答案
相关题目