题目内容
【题目】如图，在平面直角坐标系中，矩形ABCD的顶点B，C在x轴上，A，D在第一象限，反比例函数y=
（x＞0）的图象经过点A，交CD于点E，OB=2，AB=3．
（1）求k的值；
（2）若点E恰好是DC的中点．
①求直线AE的函数解析式；
②根据图象回答，在第一象限内，当x取何值时，反比例函数的函数值大于直线AE对应函数的函数值？
③若直线AE与x轴交于点M，与y轴交于点N，请你判断线段AN与线段ME的大小关系，并说明理由．
【答案】（1）6；（2）①y=﹣
x+
；② 0＜x＜2或x＞4；③AN=ME．
【解析】分析：（1）求得A的坐标，代入反比例函数的解析式即可求得k的值；
（2）E的纵坐标是
，代入反比例函数的解析式即可求得E的坐标，从而求得矩形的边长AD和BC．①利用待定系数法即可直接求解；②根据函数图象，反比例函数的函数值大于直线AE对应函数的函数值，即求反比例函数图象在一次函数图象上边部分x的范围；③延长DA交y轴于点F，利用勾股定理分别求得AN和ME的长，即可判断．
本题解析：
（1）∵OB=2，AB=3，
∴A的坐标是（2，3），
把A（2，3）代入y=
得：k=6；
（2）E恰好是DC的中点，则E的纵坐标是
，把y=
代入y=
得：x=4，
则E的坐标是（4， 
）．
①设直线AE的解析式是y=kx+b，
根据题意得：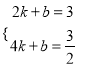 
，
解得： 
，
则直线AE的解析式是y=﹣
x+
；
②根据图象回答，在第一象限内，当0＜x＜2或x＞4时，反比例函数的函数值大于直线AE对应函数的函数值；
③延长DA交y轴于点F．
则AF⊥y轴，AF=2，F的坐标是（0，3），OF=3．
在y=﹣
x+
中，令x=0，解得y=
，即N的坐标是（0， 
），NF=
﹣3=
；
令y=0，解得：x=6，则M的坐标是（6，0）．则CM=2．
则AN=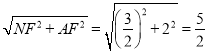
，
ME=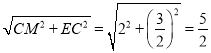
．
则AN=ME．
