题目内容
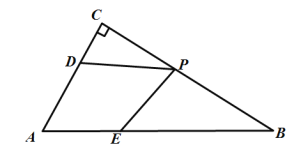
【题目】（1）模型探究：如图1，
、
、
分别为
三边
、
、
上的点，且
，
与
相似吗？请说明理由.
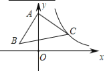
（2）模型应用：为等边三角形，其边长为
，为边上一点，为射线上一点，将
沿
翻折，使点
落在射线
上的点处，且
.
①如图2，当点在线段上时，求
的值；
②如图3，当点落在线段的延长线上时，求与的周长之比.
【答案】（1）
，见解析；（2）①
；②
与
的周长之比为
.
【解析】
（1）根据三角形的内角和得到
，即可证明；
（2）①设
，
，根据等边三角形的性质与折叠可知
，
，
，根据三角形的内角和定理得，即可证明，故
，再根据比例关系求出
的值；
②同理可证，得，得
，再得到
，再根据相似三角形的性质即可求解.
解（1），
理由：
，
在中，
，
，
，
，
，
，
；
（2）①设，，
是等边三角形，
，
，
由折叠知，，，，
在中，，
，
，
，
，
，
，
，
，
，
，
，
，
，
；
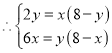②设，，
是等边三角形，
，，
由折叠知，，，，
在中，
，
，
，
，
，
，
，
，
，
，
，
，
，
.
.
与的周长之比为
.
练习册系列答案
相关题目
