题目内容
已知一次函数y=-
x+m(m为实数)的图象为直线l,l分别交x,y于A,B两点,以坐标原点O为 圆心的圆的半径为1.
圆心的圆的半径为1.
(1)求A、B两点的坐标(用含m的代数式表示);
(2)设点O到直线l的距离为d,试用含m的代数式表示d,并求出当直线1与⊙O相切时,m的值;
(3)当⊙O被直线l所截得的弦长等于1时,求m的值及直线l与⊙O的交点坐标.
| 3 |
 圆心的圆的半径为1.
圆心的圆的半径为1.(1)求A、B两点的坐标(用含m的代数式表示);
(2)设点O到直线l的距离为d,试用含m的代数式表示d,并求出当直线1与⊙O相切时,m的值;
(3)当⊙O被直线l所截得的弦长等于1时,求m的值及直线l与⊙O的交点坐标.
(1)当x=0时,y=m;当y=0时,x=
m
∴A点坐标为(
m,0),B点坐标为(0,m).
(2)结合图象可知:
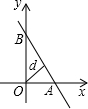 OA=
OA=
|m|,OB=|m|,
在Rt△OAB中,无论m(m≠0)取何值,
都有tan∠BAO=
=
,∴∠BAO=60°
当m=0时,也可推得直线1与x轴成60°角,又d是Rt△OAB斜边上的高,
∴d=
|m|,
∵⊙O的半径等于1,∴
|m|=1,
∴m=±2.
(3)由(2)推出∠BAO=60°.又l被⊙O所截得的弦长等于半径1,结合圆的性质可知1过⊙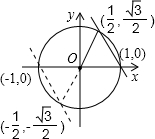 O与x轴的交点(1,0)或(-1,0)
O与x轴的交点(1,0)或(-1,0)
把(1,0)或(-1,0)代入y=-
x+m中,
可求得m=±
从而得1与⊙O的另一交点坐标为(
,
)或(-
,-
)
| ||
| 3 |
∴A点坐标为(
| ||
| 3 |
(2)结合图象可知:
 OA=
OA=
| ||
| 3 |
在Rt△OAB中,无论m(m≠0)取何值,
都有tan∠BAO=
| OB |
| OA |
| 3 |
当m=0时,也可推得直线1与x轴成60°角,又d是Rt△OAB斜边上的高,
∴d=
| 1 |
| 2 |
∵⊙O的半径等于1,∴
| 1 |
| 2 |
∴m=±2.
(3)由(2)推出∠BAO=60°.又l被⊙O所截得的弦长等于半径1,结合圆的性质可知1过⊙
 O与x轴的交点(1,0)或(-1,0)
O与x轴的交点(1,0)或(-1,0)把(1,0)或(-1,0)代入y=-
| 3 |
可求得m=±
| 3 |
从而得1与⊙O的另一交点坐标为(
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |

练习册系列答案
相关题目




 单位的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
单位的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.