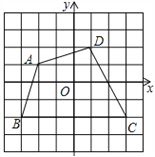
题目内容
【题目】如图,在平面直角坐标系,A(a,0),B(b,0),C(﹣1,2),且|2a+b+1|+(a+2b﹣4)2=0.
(1)求a,b的值;
(2)①在x轴的正半轴上存在一点M,使S△COM=![]() △ABC的面积,求出点M的坐标;
△ABC的面积,求出点M的坐标;
②在坐标轴的其他位置是否存在点M,使△COM的面积=![]() △ABC的面积仍然成立?若存在,请直接写出符合条件的点M的坐标为 .
△ABC的面积仍然成立?若存在,请直接写出符合条件的点M的坐标为 .

【答案】(1)a=﹣2,b=3(2)①M(![]() ,0)②(﹣
,0)②(﹣![]() ,0),(0,5),(0,﹣5).
,0),(0,5),(0,﹣5).
【解析】试题分析:(1)由绝对值和偶次方的非负性列出二元一次方程组,解方程组即可得出a,b的值,
(2)①先求出△ABC的面积,再利用△COM的面积是△ABC面积的![]() ,求出点M的坐标.
,求出点M的坐标.
②利用△COM的面积是△ABC面积的![]() ,分别求出M在x轴负半轴上的坐标和在y轴上的坐标即可.
,分别求出M在x轴负半轴上的坐标和在y轴上的坐标即可.
解:(1)∵|2a+b+1|+(a+2b﹣4)2=0,
又∵|2a+b+1|和(a+2b﹣4)2都是非负数,
所以得![]() ,
,
解方程组得,![]() ,
,
∴a=﹣2,b=3.
(2)①由(1)得A,B点的坐标为A(﹣2,0),B(3,0),|AB|=5.
∵C(﹣1,2),
∴△ABC的AB边上的高是2,
∴![]() .
.
要使△COM的面积是△ABC面积的![]() ,而C点不变,即三角形的高不变,M点在x轴的正半轴上,只需使
,而C点不变,即三角形的高不变,M点在x轴的正半轴上,只需使![]() .
.
此时![]() .
.
∴M点的坐标为![]()
②由①中![]() 的对称点得
的对称点得![]() ,
,
当M在y轴上时,△COM的高为1,
∵△COM的面积=![]() △ABC的面积,
△ABC的面积,
∴![]() |OM|×1=
|OM|×1=![]()
∴OM=±5,
∴M2(0,5)M3(0,﹣5).
故答案为:(﹣![]() ,0),(0,5),(0,﹣5).
,0),(0,5),(0,﹣5).

练习册系列答案
相关题目