题目内容
【题目】有一些相同的房间需要粉刷墙面,一天3名师傅去粉刷8个房间,结果其中有40㎡墙面未来得及刷;同样时间内5名徒弟粉刷了9个房间的墙面,每名师傅比徒弟一天多刷30㎡墙面.
(1)求每个房间需要粉刷的墙面面积;
(2)张老板现有36个这样的房间需要粉刷,若请1名师傅带2名徒弟去,需几天完成?
(3)已知每名师傅、徒弟每天的工资分别是85元、65元,张老板要求在3天内(包括3天)完成36个房间的粉刷,问如何在这8人中雇用人员(不一定8人全部雇用),才合算呢?
【答案】
【解析】
试题(1)中可利用“每个房间需要粉刷的墙面面积”作为相等关系列方程求出徒弟和师傅的工作效率,再代入求每个房间需要粉刷的墙面面积;
(2)直接利用工作总量除以工作效率可求出工作时间;
(3)根据师傅与徒弟的工资以及工作效率分别分析得出即可.
试题解析:(1)设每个房间需要粉刷的墙面面积为x m2.
由题意得,![]() ,
,
解得:x=50.
答:设每个房间需要粉刷的墙面面积为50m2.
(2)由(1)设每位师傅每天粉刷的墙面面积为![]() =120m2,
=120m2,
每位徒弟每天粉刷的墙面面积为120-30=90m2,
1个师傅带两个徒弟粉刷36个房间需要50×36÷(120+180)=6天.
答:若请1名师傅带2名徒弟去,需要6天完成.
(3)第一种情况:
假设1个师傅干3天,则:1×3×120=360平,师傅的费用是3×85=255; 还余50×36-360=1440平,需要徒弟的人次是:1440÷90=16(人次),这时不能按时完成任务;
第二种情况:
假设2个师傅干3天,则:2×3×120=720平,师傅的费用是3×85×2=510(元);还余50×36-720=1080平,需要徒弟的人次是:1080÷90=12(人次),则4个徒弟干3天,4×90×3=1080平,费用是4×65×3=780元,总费用是510+780=1290元;
第三种情况:
师傅2人徒弟4人同时干3天省钱.设雇m名师傅,n名徒弟,工资为B:
式1:m×3×120+n×3×90=36×50=1800,
即:4m+3n=20①,
得:n=(20-4m),
式2:3×85×m+3×65×n=B,
把n代入得:B=1300-5m②,
∵m,n均为整数,徒弟每天的工资比师傅每天的工资少,
∴师傅2名,再雇4名徒弟才合算.
答:在这8个人中雇2个师傅,再雇4名徒弟最合算.

【题目】为了了解某市九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:50分; B:49-45分;C:44-40分;D:39-30分;E:29-0分).每段包含最高分,不包含最低分,统计表如下,统计图如图所示.
分数段 | 频数(人) | 百分比 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
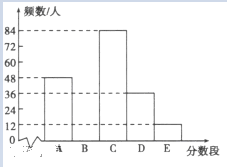
根据上面提供的信息,回答下列问题:
(1)在统计表中,![]() 的值为___,
的值为___, ![]() 的值为__,并将统计图补充完整.
的值为__,并将统计图补充完整.
(2)成绩在40分以上定为优秀,那么该市今年10440名九年级学生中体育成绩为优秀的学生约有多少名?