题目内容
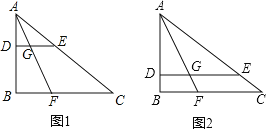
【题目】在Rt△ABC中,∠B=90°,点F在边BC上,tan∠FAC=![]() ,点E为斜边AC上一动点,ED⊥AB于点D,交AF于点G.
,点E为斜边AC上一动点,ED⊥AB于点D,交AF于点G.
(1)如图1,求证:![]() ;
;
(2)如图1,若AB=2DE,求证:![]() BF+AD=2GE;
BF+AD=2GE;
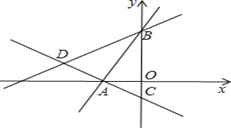
(3)如图2,若AB=DE=4,AD=3,直接写出FC的长 .
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)由题意可得DE∥BC,可得△ADG∽△ABF,△AGE∽△AFC,由相似三角形性质可得![]() ,
,![]() ,可得结论;
,可得结论;
(2)在DB上截取DM=![]() BF,连接EM交AF于点N,通过证明△ABF∽△EDM,可得∠DME=∠AFB,∠BAF=∠DEM,可证∠ANE=90°,通过证明△AMN∽△EGN,可得
BF,连接EM交AF于点N,通过证明△ABF∽△EDM,可得∠DME=∠AFB,∠BAF=∠DEM,可证∠ANE=90°,通过证明△AMN∽△EGN,可得![]() ,由线段的和差关系,可得结论;
,由线段的和差关系,可得结论;
(3)过点F作FM⊥AC于点M,由勾股定理可求AE=5,由题意可证△ADE∽△ABC,可得![]() =
=![]() ,可求AC,BC的长,由锐角三角函数可求AM=2FM,MC=
,可求AC,BC的长,由锐角三角函数可求AM=2FM,MC=![]() FM,即可求FM的长,由勾股定理可求FC的长.
FM,即可求FM的长,由勾股定理可求FC的长.
(1)∵ED⊥AB,
∴∠ADE=90°,
∵∠B=90°,
∴∠B=∠ADE,
∴DE∥BC,
∴△ADG∽△ABF,△AGE∽△AFC
∴![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
(2)如图,在DB上截取DM=![]() BF,连接EM交AF于点N,
BF,连接EM交AF于点N,
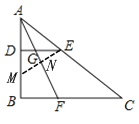
∵AB=2DE,DM=![]() BF,
BF,
∴![]() =
=![]() ,且∠ABF=∠EDM=90°
,且∠ABF=∠EDM=90°
∴△ABF∽△EDM
∴∠DME=∠AFB,∠BAF=∠DEM
∵∠BAF+∠AFB=90°
∴∠BAF+∠DME=90°
∴∠ANE=90°,
∵tan∠FAC=![]() =
=![]()
∵∠ANM=∠ANE,∠BAF=∠DEM
∴△AMN∽△EGN
∴![]()
∴AM=2GE,且AM=AD+DM=AD+![]() BF
BF
∴![]() BF+AD=2GE;
BF+AD=2GE;
(3)如图,过点F作FM⊥AC于点M,
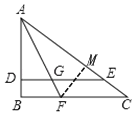
∵AD=3,DE=4,AD⊥DE
∴AE=5,
∵DE∥BC
∴△ADE∽△ABC
∴![]() =
=![]()
即![]() =
=![]()
∴AC=![]() ,BC=
,BC=![]()
∵tan∠FAC=![]() =
=![]()
∴AM=2FM,
∵tan∠C=![]()
∴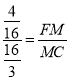
∴MC=![]() FM
FM
∵AM+MC=AC
∴2FM+![]() FM=
FM=![]()
∴FM=2,
∴MC=![]()
∴FC=![]() =
=![]()
故答案为:![]()

 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案