题目内容
【题目】四边形ABCD中,∠BAD的角平分线与边BC交于点E,∠ADC的角平分线交直线AE于点O.
(1)若点O在四边形ABCD的内部,
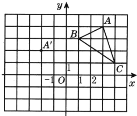
①如图1,若AD∥BC,∠B=40°,∠C=70°,则∠DOE= °;
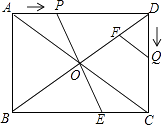
②如图2,试探索∠B、∠C、∠DOE之间的数量关系,并将你的探索过程写下来.
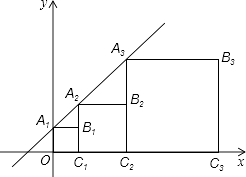
(2)如图3,若点O在四边形ABCD的外部,请你直接写出∠B、∠C、∠DOE之间的数量关系.
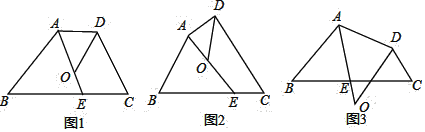
【答案】(1)①125;②∠B+∠C+2∠DOE=360°,理由详见解析;(2)∠B+∠C=2∠DOE,理由详见解析.
【解析】
(1)①根据平行线的性质和角平分线的定义可求∠BAE,∠CDO,再根据三角形外角的性质可求∠AEC,再根据四边形内角和等于360°可求∠DOE的度数;
②根据三角形外角的性质和角平分线的定义可得∠DOE和∠BAD、∠ADC的关系,再根据四边形内角和等于360°可求∠B、∠C、∠DOE之间的数量关系;
(2)根据四边形和三角形的内角和得到∠BAD+∠ADC=360°-∠B-∠C,∠EAD+∠ADO=180°-∠DOE,根据角平分线的定义得到∠BAD=2∠EAD,∠ADC=2∠ADO,于是得到结论.
解:(1)①∵AD∥BC,∠B=40°,∠C=70°,
∴∠BAD=140°,∠ADC=110°,
∵AE、DO分别平分∠BAD、∠CDA,
∴∠BAE=70°,∠ODC=55°,
∴∠AEC=110°,
∴∠DOE=360°-110°-70°-55°=125°;
故答案为:125;
②∠B+∠C+2∠DOE=360°,
理由:∵∠DOE=∠OAD+∠ADO,
∵AE、DO分别平分∠BAD、∠CDA,
∴2∠DOE=∠BAD+∠ADC,
∵∠B+∠C+∠BAD+∠ADC=360°,
∴∠B+∠C+2∠DOE=360°;
(2)∠B+∠C=2∠DOE,
理由:∵∠BAD+∠ADC=360°-∠B-∠C,∠EAD+∠ADO=180°-∠DOE,
∵AE、DO分别平分∠BAD、∠CDA,
∴∠BAD=2∠EAD,∠ADC=2∠ADO,
∴∠BAD+∠ADC=2(∠EAD+∠ADO),
∴360°-∠B-∠C=2(180°-∠DOE),
∴∠B+∠C=2∠DOE.