Question

【题目】如图，在直角坐标系中，点的坐标为，，且．

求经过，，三点的抛物线的解析式．

在中抛物线的对称轴上是否存在点，使的周长最小？若存在，求出点的坐标；若不存在，请说明理由．

若点为抛物线上一点，点为对称轴上一点，是否存在点，使得，，，构成的四边形是平行四边形？若存在，求出点的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）抛物线解析式为;（2）存在,点C的坐标为.（3）存在,点M的坐标为:、.

【解析】

试题分析: （1）先确定出点B坐标，再用待定系数法即可；

（2）先判断出使△BOC的周长最小的点C的位置，再求解即可；

（3）分OA为对角线和为边两种情况进行讨论计算．

试题解析:

（1）过点B作BD⊥x轴于点D，由已知可得：OB=OA=2，∠BOD=60°，

在Rt△OBD中，∠ODB=90°，∠OBD=30°

∴OD=1，DB=

∴点B的坐标是（1，）．

设所求抛物线的解析式为，

由已知可得：，

解得：

∴所求抛物线解析式为.

（2）存在，

∵

又∵OB=2

∴要使△BOC的周长最小，必须BC+CO最小，

∵点O和点A关于对称轴对称

∴连接AB与对称轴的交点即为点C

且有OC=OA

此时；

点C为直线AB与抛物线对称轴的交点

设直线AB的解析式为，

将点分别代入，得：

，

解得：，

∴直线AB的解析式为，

当x=﹣1时，y=，

∴所求点C的坐标为.

（3）①当以OA为对角线时

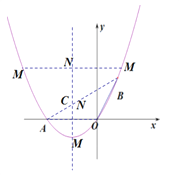
OA与MN互相垂直且平分

∴点M

②当以OA为边时

OA=MN且OA//MN

即MN=2,MN//x轴

设N（-1，t）

则M（-3，t）或（1，t）

综上：点M的坐标为：、