题目内容
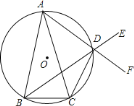
【题目】如图,已知![]() 是
是![]() 的外接圆,
的外接圆,![]() ,
,![]() 是劣弧
是劣弧![]() 上的点(不与点
上的点(不与点![]() 、
、![]() 重合),延长
重合),延长![]() 至
至![]() .
.
![]() 求证:
求证:![]() 的延长线
的延长线![]() 平分
平分![]() ;
;
![]() 若
若![]() ,
,![]() 中
中![]() 边上的高为
边上的高为![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)见解析;(2)![]() 的外接圆的面积为
的外接圆的面积为![]() .
.
【解析】
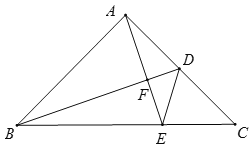
(1)要证明AD的延长线平分∠CDE,即证明∠EDF=∠CDF,转化为证明∠ADB=∠CDF,再根据A,B,C,D四点共圆的性质,和等腰三角形角之间的关系即可得到.
(2)求△ABC外接圆的面积.只需解出圆半径,故作等腰三角形底边上的垂直平分线即过圆心,再连接OC,根据角之间的关系在三角形内即可求得圆半径,可得到外接圆面积.
![]() 证明:如图,设
证明:如图,设![]() 为
为![]() 延长线上一点,
延长线上一点,

∵![]() ,
,![]() ,
,![]() ,
,![]() 四点共圆,
四点共圆,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
即![]() 的延长线平分
的延长线平分![]() .
.
![]() 设
设![]() 为外接圆圆心,连接
为外接圆圆心,连接![]() 比延长交
比延长交![]() 于
于![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,

∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() ,
,
设圆半径为![]() ,
,
则![]() ,
,
∵![]() 中
中![]() 边上的高为
边上的高为![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() 的外接圆的面积为:
的外接圆的面积为:![]() .
.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目