题目内容
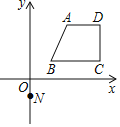
【题目】如图，过点N（0，-1）的直线y=kx+b与图中的四边形ABCD有不少于两个交点，其中A（2，3）、B（1，1）、C（4，1）、D（4，3），则k的取值范围____________
【答案】
＜k≤2．
【解析】
直线y=kx+b过点N（0，-1），则b=-1，y=kx-1．当直线y=kx-1的图象过A点时，求得k的值；当直线y=kx-1的图象过B点时，求得k的值；当直线y=kx-1的图象过C点时，求得k的值，最后判断k的取值范围．
∵直线y=kx+b过点N（0，-1），
∴b=-1，
∴y=kx-1．
当直线y=kx-1的图象过A点（2，3）时，
2k-1=3，k=2；
当直线y=kx-1的图象过B点（1，1）时，
k-1=1，k=2；
当直线y=kx-1的图象过C点（4，1）时，
4k-1=1，k=，
∴k的取值范围是＜k≤2．
故答案为＜k≤2．
【题目】某中学七、八年级各选
名同学参加“创全国文明城市”知识竞赛,计分分制,选手得分均为整数,成绩达到
分或分以上为合格,达到
分或分以上为优秀,这次竞赛后,七、八年级两支代表队成绩分布的条形统计图和成绩分析表如下,其中七年级代表队得分、分选手人数分别为
,
．
队列 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
七年级 |
|
|
|
|
|
八年级 |
|
|
|
|
|
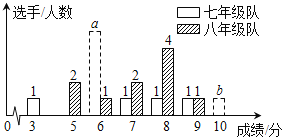
(1)根据图表中的数据,求,
的值.
(2)直接写出表中的
,
．
(3)你是八年级学生,请你给出两条支持八年级队成绩好的理由．
【题目】甲、乙两名队员参加射击训练，每人射击10次，成绩分别如下：
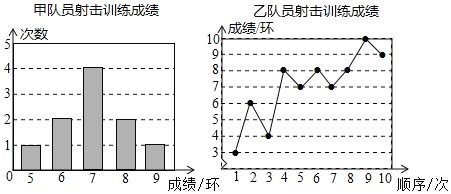
根据以上信息，整理分析数据如下：
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 |
| 7 | 7 | 1.2 |
乙 | 7 |
|
| 4.2 |
（1）
__________；
_____________；
__________；
（2）填空：（填“甲”或“乙”）
①从平均数和中位数的角度来比较，成绩较好的是__________；
②从平均数和众数的角度来比较，成绩较好的是_________________；
③成绩相对较稳定的是______________.
