Question

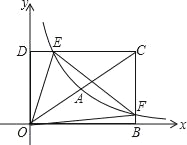
【题目】如图，矩形的中，，，动点、分别以、的速度从点、同时出发，点从点向点移动.

(1)若点从点移动到点停止，点、分别从点、同时出发，问经过时、两点之间的距离是多少？

(2)若点从点移动到点停止，点随之停止移动，点、分别从点、同时出发，问经过多长时间、两点之间的距离是？

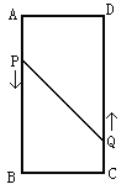
(3)若点沿着移动，点、分别从点、同时出发，点从点移动到点停止时，点随之也停止移动，试探求经过多长时间△的面积为2？

Answer 1

【答案】经过时、两点之间的距离是；经过或、两点之间的距离是；经过秒或秒的面积为．

【解析】

（1）作PE⊥CD于E，表示出PQ的长度，利用PE2+EQ2=PQ2列出方程求解即可；

（2）设x秒后，点P和点Q的距离是10cm．在Rt△PEQ中，根据勾股定理列出关于x的方程（16﹣5x）2=64，通过解方程即可求得x的值；

（3）分类讨论：①当点P在AB上时；②当点P在BC边上；③当点P在CD边上时．

（1）过点P作PE⊥CD于E．则根据题意，得：

EQ=16﹣2×3﹣2×2=6（cm），PE=AD=6cm；

在Rt△PEQ中，根据勾股定理，得：PE2+EQ2=PQ2，即36+36=PQ2，∴PQ=6cm；

∴经过2s时P、Q两点之间的距离是6cm；

（2）设x秒后，点P和点Q的距离是10cm．

（16﹣2x﹣3x）2+62=102，即（16﹣5x）2=64，∴16﹣5x=±8，∴x1=，x2=；

∴经过s或sP、Q两点之间的距离是10cm；

（3）连接BQ．设经过ys后△PBQ的面积为12cm2．

①当0≤y≤时，则PB=16﹣3y，∴PBBC=12，即×（16﹣3y）×6=12，解得：y=4；

②当＜y≤时，BP=3y﹣AB=3y﹣16，QC=2y，则

BPCQ=（3y﹣16）×2y=12，解得：y1=6，y2=﹣（舍去）；

③＜y≤8时，QP=CQ﹣PC=2y﹣（3y﹣22）=22﹣y，则

QPCB=（22﹣y）×6=12，解得：y=18（舍去）．

综上所述：经过4秒或6秒△PBQ的面积为 12cm2．