Question

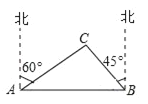
【题目】两建筑物AB和CD的水平距离为30米，如图所示，从A点测得太阳落山时，太阳光线AC照射到AB后的影子恰好在CD的墙角时的角度∠ACB=60°，又过一会儿，当AB的影子正好到达CD的楼顶D时的角度∠ADE=30°，DE⊥AB于E，则建筑物CD的高是多少米？（≈1.732，结果保留两位有效数字）

Answer 1

【答案】35m米

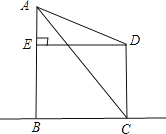
【解析】试题分析：通过投影的知识结合题意构造直角三角形，△ABC与△AED，在这两个直角三角形中，分别求出AB、AE的长；根据CD＝AB－AE计算可得建筑物CD的高．

试题解析：

解：根据题意可得：在△ABC中有：AB＝BC×tan60°＝BC＝30，

在△AED中有：∠ADE＝30°，ED＝30，

所以AE＝ED×tan30°＝，

所以CD＝EB＝AB－AE＝30≈35（米）．

故建筑物CD的高是35米．