题目内容
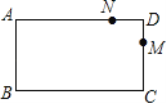
【题目】如图,矩形ABCD中,AB=4cm,BC=8cm,动点M从点D出发,按折线D﹣C﹣B﹣A﹣D方向以2cm/s的速度运动,动点N从点D出发,按折线D﹣A﹣B﹣C﹣D方向以1cm/s的速度运动.若动点M、N同时出发,相遇时停止运动,若点E在线段BC上,且BE=3cm,经过_____秒钟,点A、E、M、N组成平行四边形.
【答案】![]()
【解析】
根据t的值讨论M、N的位置,根据平行四边形的判定定理即可求解.
如图,
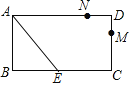
在直角△ABE中,AE=![]() =5cm.
=5cm.
设运动的时间是t秒.
当0<t<2时,M在CD上,N在DA上,
若平行四边形是AEMN,
则AE∥MN且AE=MN,而AE=MN不可能成立;
当t=2时,M在C点,DN=4cm,
此时,AN≠EC,
则不能构成平行四边形;
当2<t<4.5时,M在BC上,
则EM=BC+CD-BE-2t=9-2t,AN=8-t,
当9-2t=8-t时,
解得:t=1(舍去),
当4.5<t<6时,M在BC上,
则EM=2t-(BC+CD-BE)=2t-9,AN=8-t,
当2t-9=8-t时,
解得:t=![]() ,
,
此时四边形AMEN是平行四边形;
当6<t<8时,M在AB上,N在AD上,
不能构成平行四边形;
当t=8时,Q与A重合,不能构成平行四边形形.
综上所述:经过![]() 秒钟,点A、E、M、N组成平行四边形.
秒钟,点A、E、M、N组成平行四边形.
故答案为:![]() .
.

【题目】2019年1月有300名教师参加了“新技术支持未来教育”培训活动,会议就“面向未来的教育”和“家庭教育”这两个问题随机调查了60位教师,并对数据进行了整理、描述和分析.下面给出了部分信息:
a.关于“家庭教育”问题发言次数的频数分布直方图如下(数据分成6组:0≤x<4,4≤x<8,8≤x<12,12≤x<16,16≤x<20,20≤x≤24):
b.关于“家庭教育”问题发言次数在8≤x<12这一组的是:
8899910101010101011111111
c.“面向未来的教育”和“家庭教育”这两问题发言次数的平均数、众数、中位数如下:
问题 | 平均数 | 中位数 | 众数 |
面向未来的学校教育 | 11 | 10 | 9 |
家庭教育 | 12 | m | 10 |
根据以上信息,回答下列问题:
(1)表中m的值为______;
(2)在此次采访中,参会教师更感兴趣的问题是______(填“面向未来的教育”或“家庭教育”),理由是______;
(3)假设所有参会教师都接受调查,估计在“家庭教育”这个问题上发言次数超过8次的参会教师有______位.

【题目】车间有20名工人,某天他们生产的零件个数统计如下表.
车间20名工人某一天生产的零件个数统计表
生产零件的个数(个) | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 19 | 20 |
工人人数(人) | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
(1)求这一天20名工人生产零件的平均个数;
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?