��Ŀ����
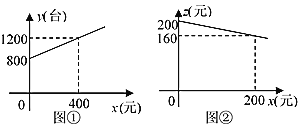
����Ŀ����ͼ1��P��m��n����������y=ax2-4ax��a��0���ϣ�EΪ�����ߵĶ��㣮
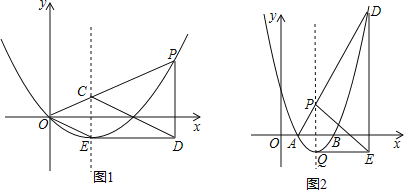
��1�����E�����꣨�ú�a��ʽ�ӱ�ʾ����
��2������P�ڵ�һ���ޣ��߶�OP�������ߵĶԳ����ڵ�C���������ߵĶ���E��x���ƽ����DE������P��x��Ĵ��߽�DE�ڵ�D������CD����֤��CD��OE��
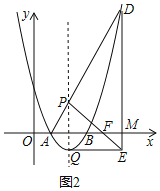
��3����ͼ2����a=1���ҽ�ͼ1�е�����������ƽ��3����λ����x�ύ��A��B���㣬ƽ�ƺ�������ߵĶ���ΪQ��P����x���Ϸ��ĶԳ����ϵĶ��㣬ֱ��AP������������һ��D���ֱ��Q��D��x�ᡢy���ƽ���߽��ڵ�E���ҡ�EPQ=2��APQ�����P�����꣮
���𰸡�(1) E��2����4a����(2)������;(3) P��2��![]() +1����
+1����
��������
��1����ԭʽ��ȡ����ʽȻ�ɽ��
��2����ֱ��OE�Ľ���ʽΪ��y��k x����E�����ɵ�ֱ��OE�Ľ���ʽΪ��y����2ax����P��m��n����ֱ��OP�Ľ���ʽΪ��y��![]() ���õ�C��2��
���õ�C��2��![]() ����Ȼ����ֱ��CD�Ľ���ʽΪ��y��kx+b���õ���k����2a�����ɽ��
����Ȼ����ֱ��CD�Ľ���ʽΪ��y��kx+b���õ���k����2a�����ɽ��
��3����a��1ʱ�������߽���ʽΪ��y��x2��4x������ƽ��3����λ���µ������߽���ʽΪ��y��x2��4x+3����x��2��2��1��Ȼ����P��2��t�����ɵ�AP�Ľ���ʽΪ��y��tx��t��D��3+t��t2+2t����Q��2����1����E��3+t����1��������PE��x����F�����ɽ��
�⣺��1��y��ax2��4ax��a��x2��4x+4��4����a��x��2��2��4a��
��E��2����4a����
��2����ֱ��OE�Ľ���ʽΪ��y��kx��
��E��2����4a������ã�2k����4a��
k����2a��
��ֱ��OE�Ľ���ʽΪ��y����2ax��
��P��m��n����ֱ��OP�Ľ���ʽΪ��y��![]() ��
��
�൱x��2ʱ��y��![]() ����C��2��
����C��2��![]() ����
����
��D��m����4a����
��ֱ��CD�Ľ���ʽΪ��y��kx+b��
����D��C���������ã�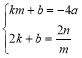 ��n��am2��4am����
��n��am2��4am����
��ã�k����2a��
������ֱ��ϵ����ȣ�
��OE��CD��
��3����ͼ2����a��1ʱ�������߽���ʽΪ��y��x2��4x��
����ƽ��3����λ���µ������߽���ʽΪ��y��x2��4x+3����x��2��2��1��
��Q��2����1����A��1��0����B��3��0����
��P��2��t����
�ɵ�AP�Ľ���ʽΪ��y��tx��t��
����������Ϊ��![]() ����ã�
����ã�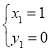 ��
��![]() ��
��
��D��3+t��t2+2t����
��Q��2����1����
��E��3+t����1����
��PQ��QE��t+1��
���EPQ��45�㣬
�ߡ�EPQ��2��APQ��
���APQ��22.5�㣬
��PE��x����F��
�ߡ�DEP��45�㣬
��ME��FM��1��
���FPA����PAF��67.5�㣬
��PF��AF��t+1��
��FP��![]() t��
t��
��![]() t��t+1��
t��t+1��
t��![]() ��
��![]() +1��
+1��
��P��2��![]() +1����
+1����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�