Question

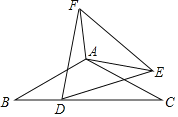
【题目】如图，已知△ABC中，∠BAC＝120°，AB＝AC＝2 ．D为BC边一点，且BD：DC＝1：2．以D为一个点作等边△DEF，且DE＝DC连接AE，将等边△DEF绕点D旋转一周，在整个旋转过程中，当AE取得最大值时AF的长为_____．

Answer 1

【答案】2

【解析】

点E，F在以D为圆心，DC为半径的圆上，当A，D，E在同一直线上时AE取最大值，过点A作AH⊥BC交BC于H，通过解直角三角形求出DH，BH，CH的长度，∠ADH的度数，证明四边形DEFC是菱形，△ACF为直角三角形，通过勾股定理可求出AF的长度．

解：如图，点E，F在以D为圆心，DC为半径的圆上，当A，D，E在同一直线上时AE取最大值，

过点A作AH⊥BC交BC于H，

∴∠BAC＝120°，AB＝AC＝2，

∴∠B＝∠ACB＝30°，BH＝CH，

∴在Rt△ABH中，

AH＝AB＝，BH＝AH＝3，

∴BC＝2BH＝6，

∵BD：DC＝1：2，

∴BD＝2，CD＝4，

∴DH＝BH﹣BD＝1，

在Rt△ADH中，AH＝，DH＝1，

∴tan∠DAH＝，

∴∠DAH＝30°，∠ADH＝60°，

∵△DEF是等边三角形，

∴∠E＝60°，DE＝EF＝DC，

∵∠ADC＝∠E＝60°，

∴DC∥EF，

∵DC＝EF，

∴四边形DEFC为平行四边形，

又∵DE＝DC，

∴平行四边形DEFC为菱形，

∴FC＝DC＝4，∠DCF＝∠E＝60°，

∴∠ACF＝ACB+∠DCF＝90°，

在Rt△ACF中，,

故答案为：．