题目内容
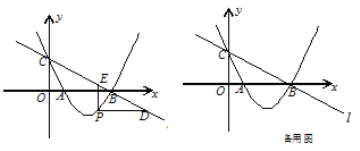
【题目】如图,在矩形ABCD中,AB=2cm,∠ADB=30°.P,Q两点分别从A,B同时出发,点P沿折线AB﹣BC运动,在AB上的速度是2cm/s,在BC上的速度是2![]() cm/s;点Q在BD上以2cm/s的速度向终点D运动,过点P作PN⊥AD,垂足为点N.连接PQ,以PQ,PN为邻边作PQMN.设运动的时间为x(s),PQMN与矩形ABCD重叠部分的图形面积为y(cm2)
cm/s;点Q在BD上以2cm/s的速度向终点D运动,过点P作PN⊥AD,垂足为点N.连接PQ,以PQ,PN为邻边作PQMN.设运动的时间为x(s),PQMN与矩形ABCD重叠部分的图形面积为y(cm2)
(1)当PQ⊥AB时,x等于多少;
(2)求y关于x的函数解析式,并写出x的取值范围;
(3)直线AM将矩形ABCD的面积分成1:3两部分时,直接写出x的值.
【答案】(1)![]() s;(2)y=
s;(2)y=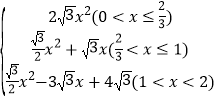 ;(3)当x=
;(3)当x=![]() s或
s或![]() 时,直线AM将矩形ABCD的面积分成1:3两部分.
时,直线AM将矩形ABCD的面积分成1:3两部分.
【解析】
(1)当PQ⊥AB时,BQ=2PB,由此构建方程即可解决问题;
(2)分三种情形分别求解即可解决问题;
(3)分两种情形分别求解即可解决问题.
解:(1)当PQ⊥AB时,BQ=2PB,
∴2x=2(2﹣2x),
∴x=![]() s.
s.
(2)①如图1中,当0<x≤![]() 时,重叠部分是四边形PQMN.
时,重叠部分是四边形PQMN.
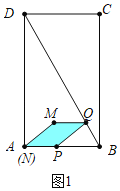
y=2x×![]() x=2
x=2![]() x2.
x2.
②如图②中,当![]() <x≤1时,重叠部分是四边形PQEN.
<x≤1时,重叠部分是四边形PQEN.

y=![]() (2﹣x+2x)×
(2﹣x+2x)×![]() x=
x=![]() x2+
x2+![]() x.
x.
③如图3中,当1<x<2时,重叠部分是四边形PNEQ.
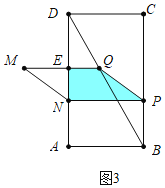
y=![]() (2﹣x+2)×[
(2﹣x+2)×[![]() x﹣2
x﹣2![]() (x﹣1)]=
(x﹣1)]=![]() x2﹣3
x2﹣3![]() x+4
x+4![]() ;
;
综上所述,y=
(3)①如图4中,当直线AM经过BC中点E时,满足条件.
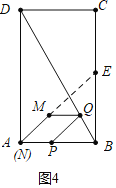
则有:tan∠EAB=tan∠QPB,
∴![]() =
=![]() ,
,
解得x=![]() .
.
②如图5中,当直线AM经过CD的中点E时,满足条件.
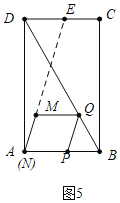
此时tan∠DEA=tan∠QPB,
∴![]() =
=![]() ,
,
解得x=![]() ,
,
综上所述,当x=![]() 或
或![]() 时,直线AM将矩形ABCD的面积分成1:3两部分.
时,直线AM将矩形ABCD的面积分成1:3两部分.
故答案为:(1)![]() s;(2)y=
s;(2)y=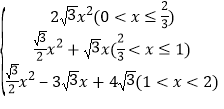 ;(3)x=
;(3)x=![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目