Question

【题目】如图，在矩形ABCD中，AB=3，BC=4，现将点A，C重合，使纸片折叠压平，折痕为EF，那么重叠部分△AEF的面积= ．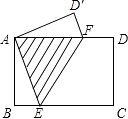

Answer 1

【答案】
【解析】解：由折叠的性质可知∠AEF=∠CEF，AE=EC，
由平行线的性质可知∠CEF=∠AFE，
∴∠AEF=∠AFE，
∴AE=AF=EC，
设AE=AF=EC=x，则BE=4﹣x，
在Rt△ABE中，由勾股定理得AB2+BE2=AE2 ，
即32+（4﹣x）2=x2 ，
解得x= ，
∴S△AEF= ×AF×AB= × ×3= ．
故本题答案为： ．
【考点精析】解答此题的关键在于理解翻折变换（折叠问题）的相关知识，掌握折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．