题目内容
【题目】如图,已知E、F、G、H分别为菱形ABCD四边的中点,AB=6cm,∠ABC=60°,则四边形EFGH的面积为__cm2.

【答案】![]() .
.
【解析】试题解析:连接AC,BD,相交于点O,如图所示,
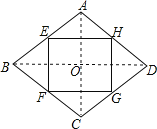
∵E、F、G、H分别是菱形四边上的中点,
∴EH=![]() BD=FG,EH∥BD∥FG,
BD=FG,EH∥BD∥FG,
EF=![]() AC=HG,
AC=HG,
∴四边形EHGF是平行四边形,
∵菱形ABCD中,AC⊥BD,
∴EF⊥EH,
∴四边形EFGH是矩形,
∵四边形ABCD是菱形,∠ABC=60°,
∴∠ABO=30°,
∵AC⊥BD,
∴∠AOB=90°,
∴AO=![]() AB=3,
AB=3,
∴AC=6,
在Rt△AOB中,由勾股定理得:OB=![]() ,
,
∴BD=6![]() ,
,
∵EH=![]() BD,EF=
BD,EF=![]() AC,
AC,
∴EH=3![]() ,EF=3,
,EF=3,
∴矩形EFGH的面积=EFFG=9![]() cm2.
cm2.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目