题目内容
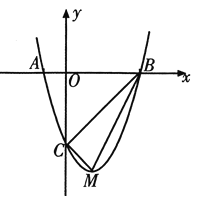
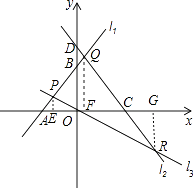
【题目】如图,已知直线l1:y=x+3与x轴交于点A,与y轴交于点B,与直线l2:y=﹣ ![]() x交于点P.直线l3:y=﹣
x交于点P.直线l3:y=﹣ ![]() x+4与x轴交于点C,与y轴交于点D,与直线l1交于点Q,与直线l2交于点R.
x+4与x轴交于点C,与y轴交于点D,与直线l1交于点Q,与直线l2交于点R. 
(1)点A的坐标是 , 点B的坐标是 , 点P的坐标是;
(2)将△POB沿y轴折叠后,点P的对应点为P′,试判断点P′是否在直线l3上,并说明理由;
(3)求△PQR的面积.
【答案】
(1)(﹣3,0);(0,3);(﹣2,1)
(2)解:点P在直线l3上
∵P(﹣2,1),且将△POB沿y轴折叠后,点P与点P关于y轴对称,
∴P(2,1),
当x=2时,代入y=﹣ ![]() x+4得y=﹣
x+4得y=﹣ ![]() ×2+4=1,
×2+4=1,
∴点P在直线l3上
(3)解:分别过点P作PE⊥x轴于F,过点Q作QF⊥x轴于F,过点R作RG⊥x轴于G,
由 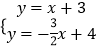 得
得 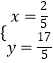 ,
,
∴Q( ![]() ,
, ![]() ),
),
由 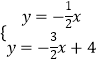 得
得 ![]()
∴R(4,﹣2),
对于y=﹣ ![]() x+4,则y=0得x=
x+4,则y=0得x= ![]() ,
,
∴C( ![]() ,0),
,0),
∴S△AQC= ![]() AC×QF=
AC×QF= ![]() ×(
×( ![]() +3)×
+3)× ![]() =
= ![]() ,S△OCR=
,S△OCR= ![]() OCGR=
OCGR= ![]() ×
× ![]() ×2=
×2= ![]() ,S△AOP=
,S△AOP= ![]() OAPE=
OAPE= ![]() ×3×1=
×3×1= ![]() ,
,
∴S△PQR=S△AQC+S△OCR﹣S△AOP= ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() .
.
【解析】解:(1)∵直线l1:y=x+3与x轴交于点A,与y轴交于点B,
∴令y=0,求得x=﹣3,令x=0,求得y=3,
∴A(﹣3,0)、B(0,3),
∵直线l1与直线l2y=﹣ ![]() x交于点P.
x交于点P.
∴解 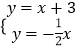 得
得 ![]() ,
,
∴P(﹣2,1),
所以答案是:(﹣3,0),(0,3),(﹣2,1);

练习册系列答案
相关题目