题目内容

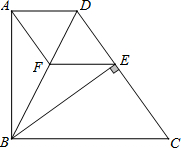
如图，在梯形ABCD中，AD∥BC，AB=3，AD=1，CD=4，∠B=50°，∠C=40°，则BC的长为（　　）
A．5B．6C．7D．8

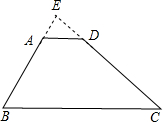
延长BA、CD交于E．∵∠B=50°，∠C=40°，
∴∠E=90°，
设AE=x，则ED=
1-x2
．
∵AD∥BC，
∵
AE
AB
=
ED
DC
，
∴
x
3
=
1-x2
4
，
∴x=
3
5
，
又∵
AE
EB
=
AD
BC
，EB=AE+AB=
3
5
+3=
18
5
，AD=1，
∴
3
5
18
5
=
1
BC
，
解得BC=6．
故选B．
练习册系列答案
相关题目
（1）如图，在△ABC中，AB=AC=6，AD是底边上的高，E为AC中点，则DE=______cm．
（2）若梯形的面积为12cm2，高为3cm，则此梯形的中位线长为______cm．
如图，在梯形ABCD中，AD∥BC，DF⊥AD，交BC于点F．若线段DF上存在点E，使∠EBC=∠EDC，且∠ECB=45°．
（1）猜想：BE与CD有什么数量关系和位置关系，并说明理由．
（2）若DE=3，DF：FC=4，求CD的长．
已知：如图，在梯形ABCD中，AB∥CD，AD=BC，过BC上一点E作直线EH，交CD于点F，交AD的延长线于点H，且EF=FH．
（1）求证：AD=DH+BE．
（2）若AB=10，CD=18，∠ADC=60°，求梯形ABCD的面积．
如图，在梯形ABCD中，AB∥CD，BD⊥AD，BC=CD，∠A=60°，CD=2cm．
（1）求cos∠CBD的值；
（2）求梯形ABCD的面积．
如图所示，在直角梯形ABCD中，AD∥BC，AD=24cm，AB=8cm，BC=26cm，动点P从A点开始沿AD边向D以1cm/s的速度运动，动点Q从C点开始沿CB边向B以3cm/s的速度运动．P，Q分别从A，C同时出发，当其中一点到端点时，另一点也随之停止运动，设运动时间为t（s），t分别为何值时，四边形PQCD是平行四边形？等腰梯形？
如图，在等腰梯形ABCD中，AB∥DC，AB=10cm，CD=4cm，点P从点A出发，以1.5cm/秒的速度沿AB向终点B运动；点Q从点C出发，以1cm/秒的速度沿CD向终点D运动（P、Q两点中，有一个点运动到终点时，所有运动即终止），设P、Q同时出发并运动了t秒：
（1）当点Q运动到点D时，PQ把梯形分成两个特殊图形是______、______；
（2）过点D作DE⊥AB，垂足为E，当四边形DEPQ是矩形时，求t的值；
（3）探索：是否存在这样的t值，使四边形PBCQ的面积是四边形APQD面积的2倍？若存在，求出t的值；若不存在，请说明理由．
以3，5，5，11为边作梯形，这样的梯形有（　　）
A．1个B．2个C．3个D．4个
如图，在直角梯形ABCD中，AD∥BC，AB⊥AD，BC=CD，BE⊥CD，垂足为E，点F在BD上，连接AF、EF．
（1）求证：DA=DE；
（2）如果AF∥CD，求证：四边形ADEF是菱形．
（3）如果∠C=60°，EC=3，求AB的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网