Question

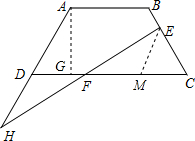
已知：如图，在梯形ABCD中，AB∥CD，AD=BC，过BC上一点E作直线EH，交CD于点F，交AD的延长线于点H，且EF=FH．
（1）求证：AD=DH+BE．
（2）若AB=10，CD=18，∠ADC=60°，求梯形ABCD的面积．

Answer 1

（1）证明：过点E作EM∥AD，交CD于点M，
∴∠H=∠FEM，
∵EF=FH，∠DFH=∠EFM，
∴△DFH≌△MFE，
∴DH=EM，
∵四边形ABCD为等腰梯形，
∴∠C=∠ADC．
∵EM∥AD，
∴∠ADC=∠EMC，
∴∠C=∠EMC．
∴EM=EC，
∴DH=EC，
∵BC=BE+EC，AD=BC，
∴AD=BE+DH；

（2）过点A作AG⊥CD于点G，
∵在梯形ABCD中，AD=BC，AB=10，CD=18，
∴DG=（18-10）÷2=4，
∵在Rt△ADG中，∠ADC=60°，
∴AG=4

3

，
∴S_梯形ABCD=

1

2

×（10+18）×4

3

=56

3

．