Question

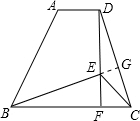
如图，在梯形ABCD中，AD∥BC，DF⊥AD，交BC于点F．若线段DF上存在点E，使∠EBC=∠EDC，且∠ECB=45°．
（1）猜想：BE与CD有什么数量关系和位置关系，并说明理由．
（2）若DE=3，DF：FC=4，求CD的长．

Answer 1

（1）BE=CD，BE⊥CD．
∵∠ECB=45°，
∴EF=FC，
在△BEF和△DCF中，

∠EBC=∠EDC ∠BFE=∠CFD EF=FC

∴△BEF≌△DCF（AAS），
延长BE交CD于G，
∵DF⊥AD，∴∠EDC+∠DCF=90°，
∵∠EBC=∠EDC，
∴∠EBC+∠DCF=90°，
∴BE⊥CD；

（2）根据题意，设DF=4x，则FC=EF=x，
∵DE=3，∴4x-x=3，
解得x=1，
∴DF=4，FC=1，
根据勾股定理，
CD=

DF2+FC2

=

42+12

=

17

．