题目内容
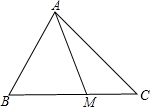如图已知点M是△ABC边BC上一点，设| AB |
| a |
| AC |
| b |
| BM |
| MC |
| AM |
| a |
| b |
（2）当
| BM |
| MC |
| AM |
| a |
| b |
（3）当
| AM |
| 4 |
| 7 |
| a |
| 3 |
| 7 |
| b |
| BM |
| MC |
考点：*平面向量
专题：
分析：（1）由
=
，
=
，根据三角形法则即可求得
，又由
=2，即可求得
的值，继而求得答案；
（2）由
=
，
=
，根据三角形法则即可求得
，又由
=m，即可求得
的值，继而求得答案；
（3）根据（2）的结论，可得
=
，继而求得m的值．
| AB |
| a |
| AC |
| b |
| BC |
| BM |
| MC |
| BM |
（2）由
| AB |
| a |
| AC |
| b |
| BC |
| BM |
| MC |
| BM |
（3）根据（2）的结论，可得
| 1 |
| m+1 |
| 4 |
| 7 |
解答：解：（1）∵
=
，
=
，
∴
=
-
=
-
，
∵
=2，
∴
=
=
（
-
）=
-
，
∴
=
+
=
+（
-
）=
+
；
（2）∵
=
，
=
，
∴
=
-
=
-
，
∵
=m，
∴
=
=
（
-
）=
-
，
∴
=
+
=
+（
-
）=
+
；
（3）∵
=
+
，
∴
=
，
解得：m=
，
∴
=
．
故答案为：（1）
+
；（2）
+
；（3）
．
| AB |
| a |
| AC |
| b |
∴
| BC |
| AC |
| AB |
| b |
| a |
∵
| BM |
| MC |
∴
| BM |
| 2 |
| 3 |
| BC |
| 2 |
| 3 |
| b |
| a |
| 2 |
| 3 |
| b |
| 2 |
| 3 |
| a |
∴
| AM |
| AB |
| BM |
| a |
| 2 |
| 3 |
| b |
| 2 |
| 3 |
| a |
| 1 |
| 3 |
| a |
| 2 |
| 3 |
| b |
（2）∵
| AB |
| a |
| AC |
| b |
∴
| BC |
| AC |
| AB |
| b |
| a |
∵
| BM |
| MC |
∴
| BM |
| m |
| m+1 |
| BC |
| m |
| m+1 |
| b |
| a |
| m |
| m+1 |
| b |
| m |
| m+1 |
| a |
∴
| AM |
| AB |
| BM |
| a |
| m |
| m+1 |
| b |
| m |
| m+1 |
| a |
| 1 |
| m+1 |
| a |
| m |
| m+1 |
| b |
（3）∵
| AM |
| 4 |
| 7 |
| a |
| 3 |
| 7 |
| b |
∴
| 1 |
| m+1 |
| 4 |
| 7 |
解得：m=
| 3 |
| 4 |
∴
| BM |
| MC |
| 3 |
| 4 |
故答案为：（1）
| 1 |
| 3 |
| a |
| 2 |
| 3 |
| b |
| 1 |
| m+1 |
| a |
| m |
| m+1 |
| b |
| 3 |
| 4 |
点评：此题考查了平面向量的知识．此题难度适中，注意掌握三角形法则的应用，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
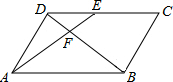如图，在平行四边形ABCD中，E为CD上一点，联结AE、BD，且AE、BD交于点F，若DE：EC=2：3，则S△DEF：S△ABF=
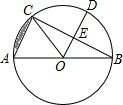如图，AB是⊙O的直径，BC是⊙O的弦，半径OD⊥BC，垂足为E，若BC=6
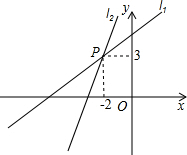如图，一次函数y=kx1+b1的图象l1与y=kx2+b2的图象l2相交于点P，则方程组