题目内容
【题目】如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,且与直线
,且与直线![]() 交于
交于![]() .
.
(1)求出点![]() 的坐标
的坐标
(2)当![]() 时,直接写出x的取值范围.
时,直接写出x的取值范围.
(3)点![]() 在x轴上,当△
在x轴上,当△![]() 的周长最短时,求此时点D的坐标
的周长最短时,求此时点D的坐标
(4)在平面内是否存在点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形?若存在,直接写出点
为顶点的四边形是平行四边形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

【答案】(1)(6,3);(2)![]() ;(3)(0,0);(4)(6,9)或(6,-3)或(-6,3).
;(3)(0,0);(4)(6,9)或(6,-3)或(-6,3).
【解析】
(1)直接联立两直线解析式,即可得到点A的坐标;
(2)直接在图象上找到![]() 时,x的取值范围;
时,x的取值范围;
(3)过点A作![]() 交点为E即可得出点D与点O重合的时候,△
交点为E即可得出点D与点O重合的时候,△![]() 的周长最短,即可得出点D的坐标;
的周长最短,即可得出点D的坐标;
(4)分三种情况考虑:当四边形OAQ1C为平行四边形时;当四边形OQ2AC为平行四边形时;当四边形OACQ3为平行四边形时,分别求出点Q的坐标即可.
(1)联立两直线解析式可得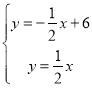
解得:![]()
![]() 点A的坐标为(6,3)
点A的坐标为(6,3)
(2)由点A(6,3)及图象知,当![]() 时,
时,![]()
(3)
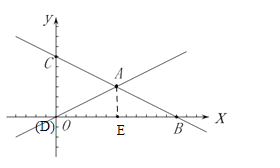
过点A作![]() 交点为E,由图可知点B关于直线AE的对称点为点O
交点为E,由图可知点B关于直线AE的对称点为点O
![]()
![]()
![]() 当点D与点O重合的时候,△
当点D与点O重合的时候,△![]() 的周长最短
的周长最短
即为CO+BC=6+6![]()
此时点D的坐标为(0,0)
(4)存在点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形
为顶点的四边形是平行四边形
如图所示,分三种情况考虑:
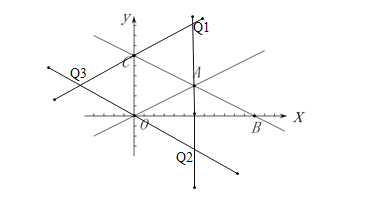
当四边形OAQ1C为平行四边形时,
点Q1的横坐标为6,纵坐标为点C的纵坐标+3=9
![]() Q1的坐标为(6,9)
Q1的坐标为(6,9)
当四边形OQ2AC为平行四边形时,
点Q2的横坐标为6,纵坐标为点A的纵坐标-6=-3
![]() Q2的坐标为(6,-3)
Q2的坐标为(6,-3)
当四边形OACQ3为平行四边形时,
点Q3关于OC的对称点为点A
![]() Q3的坐标为(-6,3)
Q3的坐标为(-6,3)
综上点Q的坐标为:(6,9)或(6,-3)或-6,3).

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目