题目内容
【题目】小丽的家和学校在一条笔直的马路旁,某天小丽沿着这条马路上学,先从家步行到公交站台甲,再乘车到公交站台乙下车,最后步行到学校(在整个过程中小丽步行的速度不变),图中折线ABCDE表示小丽和学校之间的距离y(米)与她离家时间x(分钟)之间的函数关系.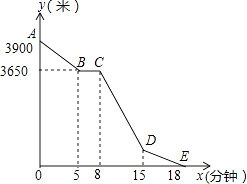
(1)求小丽步行的速度及学校与公交站台乙之间的距离;
(2)当8≤x≤15时,求y与x之间的函数关系式.
【答案】
(1)解:根据题意得:
小丽步行的速度为:(3900﹣3650)÷5=50(米/分钟),
学校与公交站台乙之间的距离为:(18﹣15)×50=150(米)
(2)解:当8≤x≤15时,设y=kx+b,
把C(8,3650),D(15,150)代入得: ![]() ,
,
解得: ![]()
∴y=﹣500x+7650(8≤x≤15)
【解析】
(1)由图像可知小丽步行的路程和时间,即可求出步行的速度及学校与公交站台乙之间的距离。
(2)观察图像当8≤x≤15时,是线段CD,得出点C、D的坐标,利用待定系数法即可求出此函数解析式。
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.

练习册系列答案
相关题目