题目内容
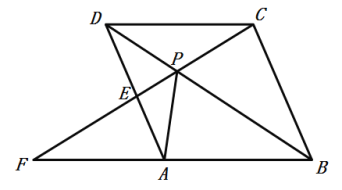
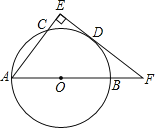
【题目】如图,AB为⊙O的直径,AC为弦,点D为![]() 中点,过点D作DE⊥直线AC,垂足为E,交AB的延长线于点F
中点,过点D作DE⊥直线AC,垂足为E,交AB的延长线于点F
(1)求证:EF是⊙O的切线;
(2)若EF=4,sin∠F=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)见解析;(2)![]() .
.
【解析】
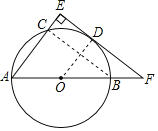
(1)如图(见解析),连接BC,OD,先根据圆周角定理得到![]() ,再根据平行线的判定可得
,再根据平行线的判定可得![]() ,然后根据垂径定理可得
,然后根据垂径定理可得![]() ,从而根据平行线的性质可得
,从而根据平行线的性质可得![]() ,最后根据圆的切线的判定即可得证;
,最后根据圆的切线的判定即可得证;
(2)先解直角三角形得到![]() ,再根据平行线的判定得出
,再根据平行线的判定得出![]() ,然后根据相似三角形的判定与性质即可得.
,然后根据相似三角形的判定与性质即可得.
(1)如图,连接BC,OD
∵AB是⊙O的直径
∴![]()
又∵![]()
∴![]()
∵点D为![]() 中点
中点
∴![]()
∴![]()
又∵OD是⊙O的半径
∴EF是⊙O的切线;
(2)在![]() 中,
中,![]()
设![]() ,则
,则![]()
由勾股定理得:![]() ,解得
,解得![]()
![]()
![]()
![]()
∴![]()
∴![]()
设⊙O的半径为![]() ,则
,则![]()
∴![]()
解得![]()
故⊙O的半径为![]() .
.

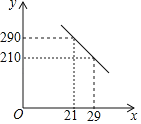
【题目】为了解高校学生对5G移动通信网络的消费意愿,从在校大学生中随机抽取了1000人进行调查,下面是大学生用户分类情况统计表和大学生愿意为5G套餐多支付的费用情况统计图(例如,早期体验用户中愿意为5G套餐多支付10元的人数占所有早期体验用户的50%).
用户分类 | 人数 |
A:早期体验用户(目前已升级为5G用户) | 260人 |
B:中期跟随用户(一年内将升级为5G用户) | 540人 |
C:后期用户(一年后才升级为5G用户) | 200人 |
下列推断中,不合理的是( )

A.早期体验用户中,愿意为5G套餐多支付10元,20元,30元的人数依次递减
B.后期用户中,愿意为5G套餐多支付20元的人数最多
C.愿意为5G套餐多支付10元的用户中,中期跟随用户人数最多
D.愿意为5G套餐多支付20元的用户中,后期用户人数最多
【题目】某儿童游乐园推出两种门票收费方式:
方式一:购买会员卡,每张会员卡费用是![]() 元,凭会员卡可免费进园
元,凭会员卡可免费进园![]() 次,免费次数用完以后,每次进园凭会员卡只需
次,免费次数用完以后,每次进园凭会员卡只需![]() 元;
元;
方式二:不购买会员卡,每次进园是![]() 元(两种方式每次进园均指单人)设进园次数为
元(两种方式每次进园均指单人)设进园次数为![]() (
( ![]() 为非负整数) .
为非负整数) .
(1)根据题意,填写下表:
进园次数(次) |
|
|
| ··· |
方式一收费(元) |
|
| ··· | |
方式二收费(元) |
| ··· |
(2)设方式一收费![]() 元,方式二收费
元,方式二收费![]() 元,分别写出
元,分别写出关于
![]() 的函数关系式;;
的函数关系式;;
(3)当![]() 时,哪种进园方式花费少?请说明理由.
时,哪种进园方式花费少?请说明理由.