题目内容
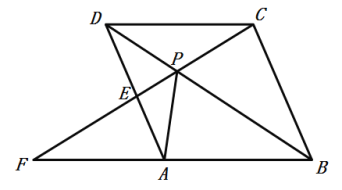
【题目】已知,如图1,在![]() 中,对角线
中,对角线![]() ,
,![]() ,
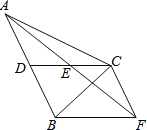
,![]() ,如图2,点
,如图2,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ;将
;将![]() 沿对角线
沿对角线![]() 剪开,
剪开,![]() 从图1的位置与点
从图1的位置与点![]() 同时出发,沿射线
同时出发,沿射线![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ,当点
,当点![]() 停止运动时,
停止运动时,![]() 也停止运动.设运动时间为
也停止运动.设运动时间为![]() ,解答下列问题:
,解答下列问题:
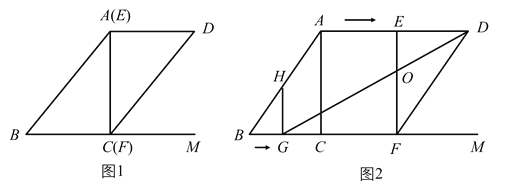
(1)当![]() 为何值时,点
为何值时,点![]() 在线段
在线段![]() 的垂直平分线上?
的垂直平分线上?
(2)设四边形![]() 的面积为
的面积为![]() ,试确定
,试确定![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)当![]() 为何值时,
为何值时,![]() 有最大值?
有最大值?
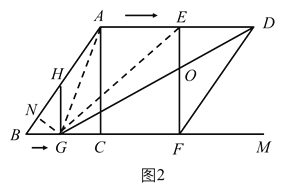
(4)连接![]() ,试求当
,试求当![]() 平分
平分![]() 时,四边形
时,四边形![]() 与四边形
与四边形![]() 面积之比.
面积之比.
【答案】(1)![]() ,(2)
,(2)![]() 四边形AHGD
四边形AHGD ![]()
(3)当![]() 四边形
四边形![]() 的面积最大,最大面积为
的面积最大,最大面积为![]()
(4)![]()
【解析】
(1)由题意得:![]() 利用垂直平分线的性质得到:
利用垂直平分线的性质得到:![]() 列方程求解即可,
列方程求解即可,
(2)![]() 四边形AHGD
四边形AHGD![]() 分别求出各图形的面积,代入计算即可得到答案,
分别求出各图形的面积,代入计算即可得到答案,
(3)利用(2)中解析式,结合二次函数的性质求最大面积即可,
(4)连接![]() 过
过![]() 作
作![]() 于
于![]() 从而求解此时时间
从而求解此时时间![]() ,分别求解四边形EGFD和四边形AHGE的面积,即可得到答案.
,分别求解四边形EGFD和四边形AHGE的面积,即可得到答案.
解:(1)如图,由题意得:![]()
![]()
![]()
![]() 及平移的性质,
及平移的性质,
![]()
![]() 点
点![]() 在线段
在线段![]() 的垂直平分线上,
的垂直平分线上,
![]()
![]()
![]()
当![]() 时,点
时,点![]() 在线段
在线段![]() 的垂直平分线上.
的垂直平分线上.

(2)![]()
![]() ,
,![]() ,
,![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
又![]()
![]()
![]()
![]() 点在
点在![]() 上,
上,
![]()
![]()
![]()
![]() 四边形AHGD
四边形AHGD![]()
![]() (
(![]() )
)
(3)![]()
![]() 四边形AHGD
四边形AHGD ![]() 且
且![]()
![]() 抛物线的对称轴是:
抛物线的对称轴是:![]()
![]() 时,
时,![]() 随
随![]() 的增大而增大,
的增大而增大,
当![]() 四边形
四边形![]() 的面积最大,最大面积为:
的面积最大,最大面积为:
![]()
(4)如图,连接![]() 过
过![]() 作
作![]() 于
于![]()
![]() 平分
平分![]()
![]()
![]()
![]()
![]()
![]()
此时:![]()
由![]()
![]()
![]() 四边形EGFD
四边形EGFD![]()
![]() 四边形ABGE
四边形ABGE![]()
![]()
![]() 四边形AHGE
四边形AHGE![]() .
.
![]() 四边形EGFD:
四边形EGFD:![]() 四边形AHGE
四边形AHGE![]()

 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
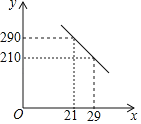
能考试全能100分系列答案【题目】某儿童游乐园推出两种门票收费方式:
方式一:购买会员卡,每张会员卡费用是![]() 元,凭会员卡可免费进园
元,凭会员卡可免费进园![]() 次,免费次数用完以后,每次进园凭会员卡只需
次,免费次数用完以后,每次进园凭会员卡只需![]() 元;
元;
方式二:不购买会员卡,每次进园是![]() 元(两种方式每次进园均指单人)设进园次数为
元(两种方式每次进园均指单人)设进园次数为![]() (
( ![]() 为非负整数) .
为非负整数) .
(1)根据题意,填写下表:
进园次数(次) |
|
|
| ··· |
方式一收费(元) |
|
| ··· | |
方式二收费(元) |
| ··· |
(2)设方式一收费![]() 元,方式二收费
元,方式二收费![]() 元,分别写出
元,分别写出关于
![]() 的函数关系式;;
的函数关系式;;
(3)当![]() 时,哪种进园方式花费少?请说明理由.
时,哪种进园方式花费少?请说明理由.