题目内容
若方程x+y=3,x-y=5和x+ky=2有公共解,则k的值是
- A.2
- B.-2
- C.1
- D.3
A
分析:把方程x+y=3,x-y=5和x+ky=2组成方程组,首先求出x,y的值,再把x,y的值代入x+ky=2中,就可以得到k的值.
解答:解;把x+y=3,x-y=5和x+ky=2组成方程组得;
 ,
,
①+②得:2x=8,
x=4,
把x=4代入①得;y=-1,
把x=4,y=-1代入③得;k=2,
∴方程组的解为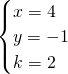 .
.
故选A.
点评:本题主要考查了三元一次方程组的解法.需要对三元一次方程组的定义有一个深刻的理解,通过解方程组,了解把“三元”转化为“二元”、把“二元”转化为“一元”的消元的思想方法,从而进一步理解把“未知”转化为“已知”和把复杂问题转化为简单问题的思想方法.解三元一次方程组的关键是消元.解题之前先观察方程组中的方程的系数特点,认准易消的未知数,消去未知数.
分析:把方程x+y=3,x-y=5和x+ky=2组成方程组,首先求出x,y的值,再把x,y的值代入x+ky=2中,就可以得到k的值.
解答:解;把x+y=3,x-y=5和x+ky=2组成方程组得;
 ,
,①+②得:2x=8,
x=4,
把x=4代入①得;y=-1,
把x=4,y=-1代入③得;k=2,
∴方程组的解为
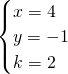 .
.故选A.
点评:本题主要考查了三元一次方程组的解法.需要对三元一次方程组的定义有一个深刻的理解,通过解方程组,了解把“三元”转化为“二元”、把“二元”转化为“一元”的消元的思想方法,从而进一步理解把“未知”转化为“已知”和把复杂问题转化为简单问题的思想方法.解三元一次方程组的关键是消元.解题之前先观察方程组中的方程的系数特点,认准易消的未知数,消去未知数.

练习册系列答案
相关题目
若方程x2-3x-2=0的两实数根为x1,x2,则
+
的值为( )
| 1 |
| x1 |
| 1 |
| x2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
若方程
=
+
有增根,则增根可能为( )
| 3 |
| x-2 |
| a |
| x |
| 4 |
| x(x-2) |
| A、0 | B、2 | C、0或2 | D、1 |
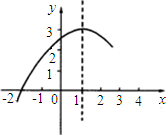 图象回答下列问题:
图象回答下列问题: