Question

附加题
（1）若方程x2-

k-1

x-1=0有两个不相等的实数根，则k的取值范围

 

．
（2）已知3-

2

的整数部分是a，小数部分是b，则a+b+

2

b

的值是

 

．
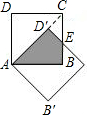
（3）如图①，已经正方形ABCD的对角线AC、BD相交于点O，E是AC上一点，连接EB，过点A作AM⊥BE，垂足为M，AM交BD于点F．
①求证：OE=OF．
②如图②，若点E在AC的延长线上，AM⊥BE于点M，交DB的延长线于点F，其它条件不变，则结论“OE=OF”还成立吗？如果成立，请给出证明，如果不成立，请说明理由．

Answer 1

分析：（1）由△＞0以及被开方数k-1≥0，即可确定k的取值范围；
（2）由1＜

2

＜2，确定a、b的值，再代入计算；
（3）①证明△AOF≌△BOE即可；②同样成立，需要证明三角形全等．

解答：解：
（1）由题意得△=k-1+4＞0，k-1≥0，
即k＞-3，k≥1，
∴k≥1；

（2）∵1＜

2

＜2，
∴a=1，b=3-

2

-1=2-

2

，
∴a+b+

2

b

=3-

2

+

2

2- 2

=3-

2

+2+

2

=5；

（3）①∵正方形ABCD的对角线AC、BD相交于点O，AM⊥BE，
∴∠AOB=∠BOE=∠AMB=90°，
∵∠AFO=∠BFM（对顶角相等），
∴∠OAF=∠OBE（等角的余角相等），
又∵OA=OB（正方形的对角线互相垂直平分且相等），
∴△AOF≌△BOE（ASA），
∴OE=OF．
②成立．
理由如下：
∠AOF=∠BOE=90°，OA=OB，（证法同①），
∵∠ABC=90°，
∴∠EBC+∠ABM=90°，
∵∠ABM+∠BAF=90°，
∴∠EBC=∠BAF，
又∵∠OAB=∠OBC=45°，
∴∠OAM=∠OBE，
∴△AOF≌△BOE（ASA），
∴OE=OF．

点评：此题综合性较强，考查了根的判别式、直角三角形、正方形的性质和三角形全等的判定等知识点．