题目内容
【题目】如图，在Rt△ABC中，∠C＝90°，∠B＝30°，点D、E分别在边AC、AB上，AD＝14，点P是边BC上一动点，当PD+PE的值最小时，AE＝15，则BE为（ ）
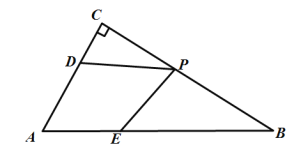
A.30B.29C.28D.27
【答案】B
【解析】
作D关于BC的对称点G，连接GE、GC，可得当PD+PE的值最小时，GE最小，然后根据直角三角形的边角关系求解即可．
解：作D关于BC的对称点G，连接GE、GC，
则PD+PE＝GE，
当PD+PE的值最小时，GE最小，
∴当GE⊥AB时，GE最小，
∵∠ACB＝90°，∠B＝30°，
∴∠A＝60°，
∵AE＝15，
∴
，
∵AD＝14，
∴CD＝CG＝
DG＝8，
∴PG＝
，
∴PE＝EG﹣PG＝
，
∴BE＝
PE＝29，
故选：B．
练习册系列答案
相关题目
