题目内容
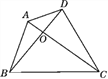
【题目】如图,在![]() 中,
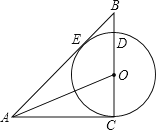
中,![]() ,点O是BC上一点,以点O圆心,OC为半径的圆交BC于点D,恰好与AB相切于点E.
,点O是BC上一点,以点O圆心,OC为半径的圆交BC于点D,恰好与AB相切于点E.
![]() 求证:AO是
求证:AO是![]() 的平分线;
的平分线;
![]() 若
若![]() ,
,![]() ,求
,求![]() 及AC的长.
及AC的长.
【答案】(1)证明见解析;(2)12cm.
【解析】
(1)由∠ACB=90°,且OC为圆O的半径,判断得到AC与圆O相切,又AB与圆O相切,根据切线长定理得到AO为∠BAC的平分线,且AE=AC;
(2)由BE为圆O的切线,BC为圆O的割线,利用切割线定理列出关系式,将BD及BE的长代入,求出BC的长,用BC-BD求出直径CD的长,进而确定出圆O的半径,由OD+BD求出OB的长,连接OE,由切线的性质得到OE垂直于BE,在直角三角形OEB中,利用锐角三角函数定义求出sinB的值,同时由OB及OE的长,利用勾股定理求出BE的长,由∠ACB=90°,OC为圆O的半径,可得出AC为圆O的切线,由AE与AC都为圆的切线,根据切线长定理得到AE=AC,设AC=AE=xcm,由AE+EB表示出AB,再由BC及AC,在直角三角形ABC中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即为AC的长.
![]() ,OC为圆O的半径,
,OC为圆O的半径,
![]() 为圆O的切线,又AB与圆O相切,E为切点,
为圆O的切线,又AB与圆O相切,E为切点,
![]() ,AO平分
,AO平分![]() ;
;
![]() 为圆O的切线,BC为圆O的割线,
为圆O的切线,BC为圆O的割线,
![]() ,又
,又![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,
![]() ,
,
连接OE,由BE为圆O的切线,得到![]() ,
,
在直角三角形BEO中,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
在直角三角形ABC中,设![]() ,则
,则![]() ,
,
![]() ,
,
根据勾股定理得:![]() ,即
,即![]() ,
,
解得:![]() ,
,
则![]() .
.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目