题目内容
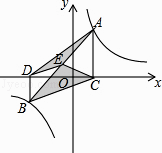
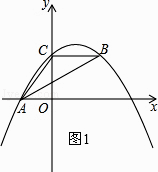
【题目】如图,抛物线y=ax2+bx+c经过A(﹣3,0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.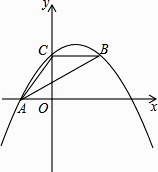
(1)求抛物线的解析式;
(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.
【答案】
(1)
解:如图1,
∵A(﹣3,0),C(0,4),
∴OA=3,OC=4.
∵∠AOC=90°,
∴AC=5.
∵BC∥AO,AB平分∠CAO,
∴∠CBA=∠BAO=∠CAB.
∴BC=AC.
∴BC=5.
∵BC∥AO,BC=5,OC=4,
∴点B的坐标为(5,4).
∵A(﹣3,0)、C(0,4)、B(5,4)在抛物线y=ax2+bx+c上,
∴ 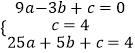 解得:
解得: 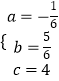
∴抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x+4
x+4
(2)
解:如图2,
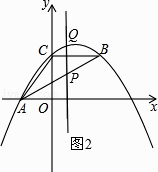
设直线AB的解析式为y=mx+n,
∵A(﹣3,0)、B(5,4)在直线AB上,
∴ ![]() 解得:
解得: 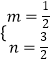
∴直线AB的解析式为y= ![]() x+
x+ ![]() .
.
设点P的横坐标为t(﹣3≤t≤5),则点Q的横坐标也为t.
∴yP= ![]() t+
t+ ![]() ,yQ=﹣
,yQ=﹣ ![]() t2+
t2+ ![]() t+4.
t+4.
∴PQ=yQ﹣yP=﹣ ![]() t2+
t2+ ![]() t+4﹣(
t+4﹣( ![]() t+
t+ ![]() )
)
=﹣ ![]() t2+
t2+ ![]() t+4﹣
t+4﹣ ![]() t﹣
t﹣ ![]()
=﹣ ![]() t2+
t2+ ![]() +
+ ![]()
=﹣ ![]() (t2﹣2t﹣15)
(t2﹣2t﹣15)
=﹣ ![]() [(t﹣1)2﹣16]
[(t﹣1)2﹣16]
=﹣ ![]() (t﹣1)2+
(t﹣1)2+ ![]() .
.
∵﹣ ![]() <0,﹣3≤t≤5,
<0,﹣3≤t≤5,
∴当t=1时,PQ取到最大值,最大值为 ![]() .
.
∴线段PQ的最大值为 ![]() .
.
(3)
解:①当∠BAM=90°时,如图3所示.
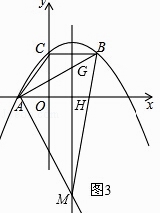
抛物线的对称轴为x=﹣ ![]() =﹣
=﹣ 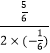 =
= ![]() .
.
∴xH=xG=xM= ![]() .
.
∴yG= ![]() ×
× ![]() +
+ ![]() =
= ![]() .
.
∴GH= ![]() .
.
∵∠GHA=∠GAM=90°,
∴∠MAH=90°﹣∠GAH=∠AGM.
∵∠AHG=∠MHA=90°,∠MAH=∠AGM,
∴△AHG∽△MHA.
∴ ![]() .
.
∴ ![]() =
= ![]() .
.
解得:MH=11.
∴点M的坐标为( ![]() ,﹣11).
,﹣11).
②当∠ABM=90°时,如图4所示.
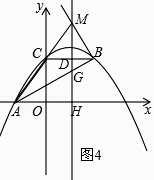
∵∠BDG=90°,BD=5﹣ ![]() =
= ![]() ,DG=4﹣
,DG=4﹣ ![]() =
= ![]() ,
,
∴BG= ![]()
= ![]()
= ![]() .
.
同理:AG= ![]() .
.
∵∠AGH=∠MGB,∠AHG=∠MBG=90°,
∴△AGH∽△MGB.
∴ ![]() =
= ![]() .
.
∴ ![]() =
= ![]() .
.
解得:MG= ![]() .
.
∴MH=MG+GH
= ![]() +
+ ![]()
=9.
∴点M的坐标为( ![]() ,9).
,9).
综上所述:符合要求的点M的坐标为( ![]() ,9)和(
,9)和( ![]() ,﹣11).
,﹣11).
【解析】(1)如图1,易证BC=AC,从而得到点B的坐标,然后运用待定系数法求出二次函数的解析式.(2)如图2,运用待定系数法求出直线AB的解析式.设点P的横坐标为t,从而可以用t的代数式表示出PQ的长,然后利用二次函数的最值性质就可解决问题.(3)由于AB为直角边,分别以∠BAM=90°(如图3)和∠ABM=90°(如图4)进行讨论,通过三角形相似建立等量关系,就可以求出点M的坐标.
【考点精析】通过灵活运用二次函数的性质,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.

【题目】某校从初二(1)班和(2)班各选拔10名同学组成甲队和乙队,参加数学竞赛活动,此次竞赛共有10道选择题,答对8题(含8题)以上为优秀,两队选手答对题数统计如下:
答对题数 | 5 | 6 | 7 | 8 | 9 | 10 | 平均数( |
甲队选手 | 1 | 0 | 1 | 5 | 2 | 1 | 8 |
乙队选手 | 0 | 0 | 4 | 3 | 2 | 1 | a |
中位数 | 众数 | 方差(s2) | 优秀率 | ||||
甲队选手 | 8 | 8 | 1.6 | 80% | |||
乙队选手 | b | c | 1.0 | m | |||
(1)上述表格中,a= ,b= ,c= ,m= .
(2)请根据平均数和众数的意义,对甲、乙两队选手进行评价.