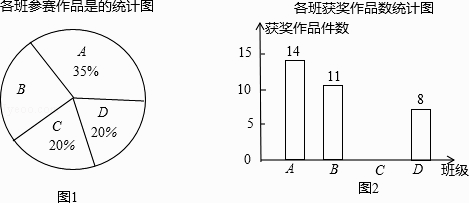
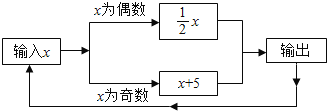
题目内容
【题目】已知:如图,四边形ABCD是任意四边形,AC与BD交于点O.试说明:AC+BD>![]() (AB+BC+CD+DA).
(AB+BC+CD+DA).
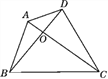
解:在△OAB中有OA+OB>AB,
在△OAD中有______________,
在△ODC中有______________,
在△________中有______________,
∴OA+OB+OA+OD+OD+OC+OB+OC>AB+AD+CD+BC,
即________________________.
∴AC+BD>![]() (AB+BC+CD+DA).
(AB+BC+CD+DA).
【答案】 OA+OD>AD, OD+OC>CD, OBC, OB+OC>BC, 2(AC+BD)>AB+BC+CD+DA
【解析】根据三角形两边之和大于第三边,得.OA+OD>AD, OD+OC>CD;在△OBC中有OB+OC>BC, 四个式子相加,得:OA+OB+OA+OD+OD+OC+OB+OC>AB+AD+CD+BC,即2(AC+BD)>AB+BC+CD+DA,从而,AC+BD>![]() (AB+BC+CD+DA).
(AB+BC+CD+DA).
得证.
故答案:OA+OD>AD, OD+OC>CD, OBC, OB+OC>BC, 2(AC+BD)>AB+BC+CD+DA.

练习册系列答案
相关题目